Waring problem
A problem in number theory formulated in 1770 by E. Waring in the following form: Any natural number is a sum of 4 squares, of 9 cubes and of 19 fourth-powers. In other words, for all 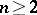 there exists a
there exists a 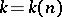 , depending only on
, depending only on  , such that every natural number is the sum of
, such that every natural number is the sum of 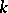
 -th powers of non-negative integers. D. Hilbert in 1909 was the first to give a general solution of Waring's problem with a very rough estimate of the value of
-th powers of non-negative integers. D. Hilbert in 1909 was the first to give a general solution of Waring's problem with a very rough estimate of the value of 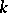 as a function of
as a function of  ; this is why the problem is sometimes known as the Hilbert–Waring problem. Let
; this is why the problem is sometimes known as the Hilbert–Waring problem. Let 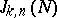 be the number of solutions of the equation
be the number of solutions of the equation
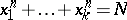 | (1) |
in non-negative integers. Hilbert's theorem then states that there exists a 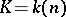 for which
for which 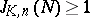 for any
for any 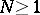 . G.H. Hardy and J.E. Littlewood, who applied the circle method to the Waring problem, demonstrated in 1928 that for
. G.H. Hardy and J.E. Littlewood, who applied the circle method to the Waring problem, demonstrated in 1928 that for 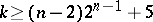 the value of
the value of 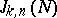 is given by an asymptotic formula of the type
is given by an asymptotic formula of the type
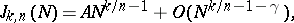 | (2) |
where 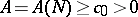 , while
, while 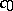 and
and 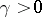 are constants. Consequently, if
are constants. Consequently, if 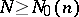 , equation (1) has a solution. This result gave rise to three problems: Determine the order of the three quantities
, equation (1) has a solution. This result gave rise to three problems: Determine the order of the three quantities 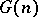 ,
, 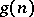 ,
, 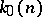 which are the smallest integers for which: a) equation (1) is solvable for
which are the smallest integers for which: a) equation (1) is solvable for 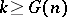 and
and 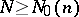 ; b) equation (1) is solvable for
; b) equation (1) is solvable for 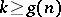 and
and 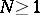 ; or c) the asymptotic formula (2) applies to
; or c) the asymptotic formula (2) applies to 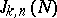 if
if 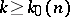 .
.
a) It is known that 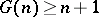 . It was proved in 1934 by I.M. Vinogradov, using his own method, that
. It was proved in 1934 by I.M. Vinogradov, using his own method, that
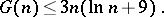 |
Moreover, many results are available concerning 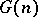 for small values of
for small values of  :
: 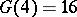 (H. Davenport, 1939);
(H. Davenport, 1939); 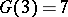 (Yu.V. Linnik, 1942).
(Yu.V. Linnik, 1942).
b) It was shown in 1936 by L. Dickson and S. Pillai, who also used the Vinogradov method, that
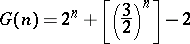 |
for all 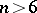 for which
for which
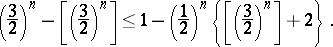 |
The last condition was demonstrated in 1957 by K. Mahler for all sufficiently large  .
.
c) The best result of all must be credited to Vinogradov, who showed that
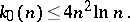 |
An elementary proof of Waring's problem was given in 1942 by Yu.V. Linnik. There exist many different generalizations of Waring's problem (the variables run through a certain subset of the set of natural numbers; the number 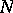 is represented by polynomials
is represented by polynomials 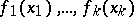 rather than by monomials
rather than by monomials 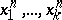 ; equation (1) is replaced by a congruence, etc.).
; equation (1) is replaced by a congruence, etc.).
The special importance of Waring's problem consists in the fact that in trying to solve it, powerful methods in analytic number theory had to be created.
References
| [1] | I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) |
| [2] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [3] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
| [4] | B.N. Delone, "The Peterburg school of number theory" , Moscow-Leningrad (1947) (In Russian) |
| [5] | A.Ya. Khinchin, "Three pearls of number theory" , Graylock (1952) (Translated from Russian) |
Comments
It is known that 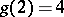 (J.L. Lagrange, 1770),
(J.L. Lagrange, 1770), 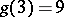 (A. Wieferich, A. Kempner, 1912),
(A. Wieferich, A. Kempner, 1912), 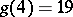 (R. Balusabramanian, J. Deshouillers, F. Dress, 1986),
(R. Balusabramanian, J. Deshouillers, F. Dress, 1986), 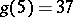 (Chen-Jingrun, 1964). See also Circle method and [a1]–[a3].
(Chen-Jingrun, 1964). See also Circle method and [a1]–[a3].
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. 6 |
| [a2] | R.C. Vaughan, "The Hardy–Littlewood method" , Cambridge Univ. Press (1981) |
| [a3] | D. Shanks, "Solved and unsolved problems in number theory" , Chelsea, reprint (1978) |
Waring problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Waring_problem&oldid=15347