Wandering point
A point 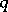 in the phase space
in the phase space 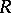 of a dynamical system
of a dynamical system 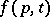 with a neighbourhood
with a neighbourhood 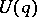 for which there exists a moment in time
for which there exists a moment in time 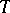 such that
such that 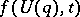 has no common points with
has no common points with 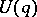 for all
for all 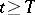 (all points of
(all points of 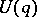 , from some moment on, leave the neighbourhood
, from some moment on, leave the neighbourhood 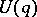 ). A point
). A point 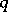 without such a neighbourhood is said to be non-wandering. This property of a point — to be wandering or non-wandering — is two-sided: If
without such a neighbourhood is said to be non-wandering. This property of a point — to be wandering or non-wandering — is two-sided: If  has no common points with
has no common points with 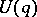 , then
, then 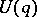 has no common points with
has no common points with 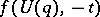 . A wandering point may become non-wandering if the space
. A wandering point may become non-wandering if the space 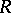 is extended. For instance, if
is extended. For instance, if 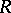 is a circle with one rest point
is a circle with one rest point  , all points of
, all points of  are wandering points. They become non-wandering if the points of some spiral without rest points, winding itself around this circle from the outside or from the inside, are added to
are wandering points. They become non-wandering if the points of some spiral without rest points, winding itself around this circle from the outside or from the inside, are added to  .
.
Comments
A set 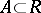 is positively recursive with respect to a set
is positively recursive with respect to a set 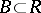 if for all
if for all 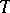 there is a
there is a 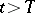 such that
such that 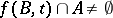 . Negatively recursive is defined analogously. A point
. Negatively recursive is defined analogously. A point  is then non-wandering if every neighbourhood of it is positively recursive with respect to itself (self-positively recursive). A point
is then non-wandering if every neighbourhood of it is positively recursive with respect to itself (self-positively recursive). A point  is positively Poisson stable (negatively Poisson stable) if every neighbourhood of it is positively recursive (negatively recursive) with respect to
is positively Poisson stable (negatively Poisson stable) if every neighbourhood of it is positively recursive (negatively recursive) with respect to 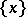 . A point is Poisson stable if it is both positively and negatively Poisson stable. If
. A point is Poisson stable if it is both positively and negatively Poisson stable. If 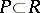 is such that every
is such that every 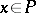 is positively or negatively Poisson stable, then all points of
is positively or negatively Poisson stable, then all points of 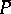 are non-wandering. See also Wandering set.
are non-wandering. See also Wandering set.
References
| [a1] | N.P. Bhatia, G.P. Szegö, "Stability theory of dynamical systems" , Springer (1970) pp. 30–36 |
Wandering point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wandering_point&oldid=15636