Wallman compactification
Wallman–Shanin compactification, 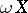 , of a topological space
, of a topological space 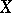 satisfying the axiom
satisfying the axiom 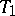 (cf. Separation axiom)
(cf. Separation axiom)
The space whose points are maximal centred systems of closed sets 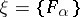 in
in 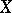 (cf. Centred family of sets). The topology in
(cf. Centred family of sets). The topology in 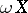 is given by the closed base
is given by the closed base 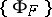 , where
, where  ranges over all closed sets in
ranges over all closed sets in 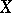 and
and 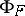 consists of precisely those
consists of precisely those 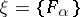 for which
for which 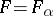 for some
for some 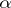 .
.
This compactification was described by H. Wallman [1].
The Wallman compactification is always a compact 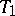 -space; for a normal space it coincides with the Stone–Čech compactification.
-space; for a normal space it coincides with the Stone–Čech compactification.
If in defining the extension 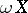 one chooses not all closed sets, but only those contained in a certain fixed closed base, one obtains a so-called compactification of Wallman type. Not every Hausdorff compactification of a Tikhonov space is a compactification of Wallman type.
one chooses not all closed sets, but only those contained in a certain fixed closed base, one obtains a so-called compactification of Wallman type. Not every Hausdorff compactification of a Tikhonov space is a compactification of Wallman type.
References
| [1] | H. Wallman, "Lattices and topological spaces" Ann of Math. , 39 (1938) pp. 112–126 |
Comments
Compactifications that are not Wallman compactifications were constructed by V.M. Ul'yanov [a1].
References
| [a1] | V.M. Ul'yanov, "Solution of a basic problem on compactifications of Wallman type" Soviet Math. Dokl. , 18 (1977) pp. 567–571 Dokl. Akad. Nauk SSSR , 233 : 6 (1977) pp. 1056–1059 |
| [a2] | R.A. Alo, H.L. Shapiro, "Normal bases and compactifications" Math. Ann. , 175 (1968) pp. 337–340 |
| [a3] | O. Frink, "Compactifications and semi-normal spaces" Amer. J. Math. , 86 (1964) pp. 602–607 |
| [a4] | R.C. Walker, "The Stone–Čech compactification" , Springer (1974) |
Wallman compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wallman_compactification&oldid=15108