WKB method
An asymptotic method of G. Wentzel, H. Kramers, L. Brillouin, and H. Jeffreys for solving ordinary differential equations of the form
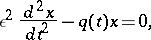 | (1) |
with a small parameter 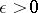 in front of the leading derivative. The method was introduced in 1926 by these workers to obtain approximate solutions of Schrödinger's quantum-mechanical wave equation (for a detailed historical account and literature see [5], [6]). Other names given to the method are Liouville–Green approximation; the method of the phase integral; the semi-classical approximation, as well as all possible combinations of the letters W, K, B (and J).
in front of the leading derivative. The method was introduced in 1926 by these workers to obtain approximate solutions of Schrödinger's quantum-mechanical wave equation (for a detailed historical account and literature see [5], [6]). Other names given to the method are Liouville–Green approximation; the method of the phase integral; the semi-classical approximation, as well as all possible combinations of the letters W, K, B (and J).
Let 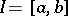 ,
, 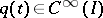 and
and 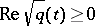 for
for 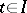 or
or 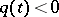 for
for 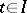 . Then there exist solutions of equation (1) such that as
. Then there exist solutions of equation (1) such that as 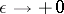 , uniformly in
, uniformly in 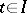 ,
,
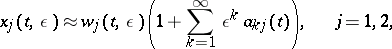 |
and
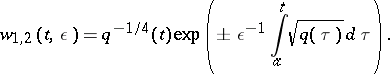 | (2) |
The principal term of the asymptotic expansion (2) is usually called the WKB approximation.
Let 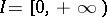 , let the above conditions on
, let the above conditions on 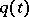 be satisfied and let
be satisfied and let
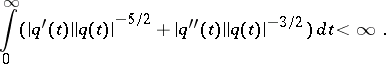 |
Then there exist solutions of equation (1) such that 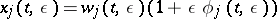 ,
, 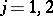 , where
, where 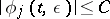 for
for 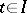 ,
, 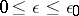 , if
, if 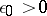 is sufficiently small, and
is sufficiently small, and 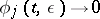 if
if 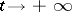 ,
, 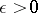 .
.
A point 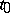 is a turning point of equation (1) if
is a turning point of equation (1) if 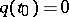 . The WKB approximation is not valid at turning points. Asymptotic formulas valid in neighbourhoods of turning points have been obtained [1], [4]. The principal term of the asymptotic expansion is expressed in the form of Bessel functions.
. The WKB approximation is not valid at turning points. Asymptotic formulas valid in neighbourhoods of turning points have been obtained [1], [4]. The principal term of the asymptotic expansion is expressed in the form of Bessel functions.
In a number of problems (the problem of eigenvalues, the dispersion problem) the asymptotic behaviour of a solution of equation (1) need to be known at interval ends only, i.e. asymptotics at turning points need not be found. If 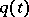 is an analytic function, it is generally possible to extend WKB formulas from one end of the interval
is an analytic function, it is generally possible to extend WKB formulas from one end of the interval 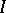 to the other through the complex plane
to the other through the complex plane 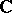 (for a rigorous proof see [2]). For entire functions
(for a rigorous proof see [2]). For entire functions 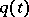 it has been found that the WKB approximation (2) is valid in certain domains of the complex plane
it has been found that the WKB approximation (2) is valid in certain domains of the complex plane 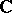 bounded by Stokes lines (i.e. by the level lines
bounded by Stokes lines (i.e. by the level lines 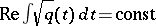 passing through the turning points). Asymptotic formulas have been obtained for the fundamental system of solutions of equation (1) which are valid throughout the complex plane except for neighbourhoods of the turning points [2].
passing through the turning points). Asymptotic formulas have been obtained for the fundamental system of solutions of equation (1) which are valid throughout the complex plane except for neighbourhoods of the turning points [2].
For WKB approximation of partial differential equations, see [5], [6], [8], [9], [10].
References
| [1] | W. Wazov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965) |
| [2] | M.A. Evgradov, M.V. Fedoryuk, "Asymptotic behaviour as 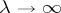 of the solution of the equation of the solution of the equation 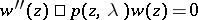 in the complex in the complex  -plane" Russian Math. Surveys , 21 : 1 (1966) pp. 1–48 Uspekhi Mat. Nauk , 21 : 1 (1966) pp. 3–50 -plane" Russian Math. Surveys , 21 : 1 (1966) pp. 1–48 Uspekhi Mat. Nauk , 21 : 1 (1966) pp. 3–50 |
| [3] | M.V. Fedoryuk, "Addendum to the Russian translation of: W. Wazov, Asymptotic expansions for ordinary differential equations, Interscience, 1965." , Moscow (1968) pp. 406–433 |
| [4] | A.A. Dorodnitsyn, "Asymptotic laws of distribution of the characteristic values for certain special forms of differential equations of the second order" Uspekhi Mat. Nauk , 7 : 6 (1952) pp. 3–96 (In Russian) |
| [5] | J. Heading, "An introduction to phase-integral methods" , Methuen (1962) |
| [6] | N. Fröman, P.O. Fröman, "JWBK-approximation" , North-Holland (1965) |
| [7] | L.D. Landau, E.M. Lifshitz, "Quantum mechanics" , Pergamon (1965) (Translated from Russian) |
| [8] | V.P. Maslov, "Théorie des perturbations et méthodes asymptotiques" , Dunod (1972) (Translated from Russian) |
| [9] | V.P. Maslov, "Operational methods" , MIR (1976) (Translated from Russian) |
| [10] | V.P. Maslov, M.V. Fedoryuk, "Semi-classical approximation in quantum mechanics" , Reidel (1981) (Translated from Russian) |
Comments
References
| [a1] | F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974) |
WKB method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=WKB_method&oldid=15871