Voting paradoxes
Voting paradoxes describe counter-intuitive election outcomes. The mathematical study started in 1770 when J.C. Borda [a1] constructed an example to argue that the plurality vote (where each voter votes for one candidate) used to select members to the French Academy of Science was flawed. Borda's example has  voters with the (complete, transitive) preferences
voters with the (complete, transitive) preferences  ,
,  with
with  , and
, and  with
with  . Here, the plurality ranking of
. Here, the plurality ranking of  conflicts with the pairwise rankings of
conflicts with the pairwise rankings of  ,
,  ,
, 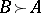 with the respective tallies of
with the respective tallies of 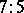 ,
,  ,
, 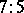 . Borda suggested an alternative method, the Borda count, where with
. Borda suggested an alternative method, the Borda count, where with  alternatives a voter's
alternatives a voter's 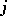 th ranked candidate receives
th ranked candidate receives 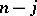 points,
points, 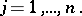 The Borda count outcome for the example is the more reasonable
The Borda count outcome for the example is the more reasonable 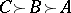 with the
with the 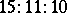 tally.
tally.
More generally, an 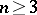 candidate election can be tallied with a voting vector
candidate election can be tallied with a voting vector 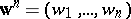 where
where 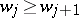 ,
,  and
and  . (The plurality vote corresponds to
. (The plurality vote corresponds to 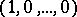 while the Borda count is
while the Borda count is 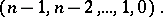 ) With the infinite number of ways to tally ballots, P.S. Laplace and other mathematicians started a two-century controversy by questioning which
) With the infinite number of ways to tally ballots, P.S. Laplace and other mathematicians started a two-century controversy by questioning which 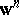 would be "optimal" . The difficulty of this area is partially captured by Arrow's assertion that no procedure does what is commonly expected (cf. Arrow impossibility theorem). See [a2], [a3] for a flavour of the rich history of this area and [a7] for a mathematical introduction.
would be "optimal" . The difficulty of this area is partially captured by Arrow's assertion that no procedure does what is commonly expected (cf. Arrow impossibility theorem). See [a2], [a3] for a flavour of the rich history of this area and [a7] for a mathematical introduction.
All paradoxes.
What makes voting paradoxes difficult to analyze is that they are "counter-intuitive" , so it is not clear what to search for. Consequently, while several paradoxes have been discovered (e.g., see [a5]), they are limited. However, by using symmetry and arguments from chaotic dynamics, all possible voting paradoxes finally have been characterized [a6], [a8]. To describe them, notice that 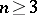 alternatives define
alternatives define 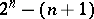 subsets with two or more candidates; for each subset, choose a voting vector. D. Saari showed that for almost-all choices of voting vectors, "anything can happen" . Namely, for each of the
subsets with two or more candidates; for each subset, choose a voting vector. D. Saari showed that for almost-all choices of voting vectors, "anything can happen" . Namely, for each of the 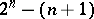 subsets, choose any ranking of the candidates. There exists an example of voters, each with a transitive ranking of the candidates, where when the ballots for each subset are tallied with the specified voting vector, the outcome is the selected one. More specifically, the vector
subsets, choose any ranking of the candidates. There exists an example of voters, each with a transitive ranking of the candidates, where when the ballots for each subset are tallied with the specified voting vector, the outcome is the selected one. More specifically, the vector 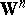 , which designates these
, which designates these 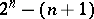 choices of voting vectors, is in an appropriate-dimensional vector space. There is a lower-dimensional algebraic set
choices of voting vectors, is in an appropriate-dimensional vector space. There is a lower-dimensional algebraic set 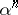 so that if
so that if 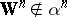 , then this "anything can happen" conclusion holds. A positive assertion is that the number and kind of paradoxes is minimized if the Borda count is used to tally each subset of candidates. More precisely, if a listing of rankings (i.e., a voting paradox) can occur with the Borda count, it also occurs with any other
, then this "anything can happen" conclusion holds. A positive assertion is that the number and kind of paradoxes is minimized if the Borda count is used to tally each subset of candidates. More precisely, if a listing of rankings (i.e., a voting paradox) can occur with the Borda count, it also occurs with any other 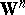 . However, if
. However, if  uses a non-Borda count choice to tally a subset of candidates, then
uses a non-Borda count choice to tally a subset of candidates, then 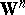 admits paradoxes that never occur with the Borda count. As an illustration, only the Borda count rankings are related with the pairwise rankings; e.g., for any other
admits paradoxes that never occur with the Borda count. As an illustration, only the Borda count rankings are related with the pairwise rankings; e.g., for any other 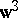 there are voters' preferences where the election outcomes are the same as in the introductory example.
there are voters' preferences where the election outcomes are the same as in the introductory example.
To illustrate the Borda count consistency advantage over other procedures, let 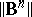 and
and 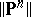 denote, respectively, the number of lists of distinct election rankings allowed by the Borda count and the plurality vote over the
denote, respectively, the number of lists of distinct election rankings allowed by the Borda count and the plurality vote over the 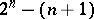 subsets. Even for
subsets. Even for 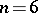 , it turns out that
, it turns out that  . These results indicate that the Borda count is the pragmatic answer to Laplace's question about the optimal choice of a voting procedure.
. These results indicate that the Borda count is the pragmatic answer to Laplace's question about the optimal choice of a voting procedure.
Statistics.
A closely related assertion holds for rankings determined by non-parametric methods of statistics. In particular, D. Haunsperger [a4] published a similar theorem, showing that for 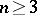 alternatives, almost-all non-parametric methods allow anything to happen. She then showed that the Krushkal–Wallis test plays the role of the Borda count by minimizing the number and kinds of paradoxes that can occur.
alternatives, almost-all non-parametric methods allow anything to happen. She then showed that the Krushkal–Wallis test plays the role of the Borda count by minimizing the number and kinds of paradoxes that can occur.
References
| [a1] | J.C. Borda, "Mémoire sur les élections au Scrutin" Histoire de l'Acad. R. des Sci. (1781) |
| [a2] | I. McLean, F. Hewitt, "Condorcet" , Edward Elgar (1994) |
| [a3] | I. McLean, A. Urken, "Classics of social choice" , Univ. Michigan Press (1995) |
| [a4] | D. Haunsperger, "Dictionaries of paradoxes for statistical tests on 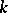 samples" J. Amer. Statist. Assoc. (1992) pp. 149–155 samples" J. Amer. Statist. Assoc. (1992) pp. 149–155 |
| [a5] | J. Kelly, "Social choice bibliography" Social Choice Welfare , 8 (1991) pp. 97–169 |
| [a6] | D.G. Saari, "A chaotic examination of aggregation paradoxes" SIAM Review , 37 (1995) pp. 37–52 |
| [a7] | D.G. Saari, "Basic geometry of voting" , Springer (1995) |
| [a8] | D.G. Saari, "The mathematical symmetry of choosing" Math. Japon. , 44 (1996) pp. 183–200 |
Voting paradoxes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Voting_paradoxes&oldid=18221