Volume form
volume element.
Let  be a vector space of dimension
be a vector space of dimension  with a given orientation and an inner product. The corresponding volume form, or volume element, is the unique element
with a given orientation and an inner product. The corresponding volume form, or volume element, is the unique element  , the space of
, the space of  -forms on
-forms on 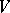 (cf. Exterior form), such that
(cf. Exterior form), such that  for each orthonormal (with respect to the given inner product) basis of
for each orthonormal (with respect to the given inner product) basis of 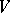 . Recall that
. Recall that 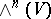 is one-dimensional. If
is one-dimensional. If 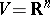 with the standard inner product and orientation, then
with the standard inner product and orientation, then 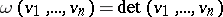 for each
for each  -tuple of vectors
-tuple of vectors  (written out in the standard basis for calculating the determinant) and
(written out in the standard basis for calculating the determinant) and 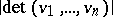 is the volume of the parallelopipedon spanned by the line segments from zero to the
is the volume of the parallelopipedon spanned by the line segments from zero to the  .
.
If  is an oriented Riemannian manifold, then the volume form
is an oriented Riemannian manifold, then the volume form  on
on  is defined by requiring that
is defined by requiring that 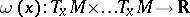 for each
for each 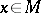 is the unique volume element on
is the unique volume element on  defined by inner product and orientation on each
defined by inner product and orientation on each  . One often writes
. One often writes 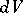 for the volume form on
for the volume form on  , even though there may not be an
, even though there may not be an  -form
-form 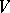 on
on  of which it is the exterior derivative.
of which it is the exterior derivative.
In given local coordinates  , let
, let 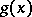 be the two-form (matrix) determining the inner product on
be the two-form (matrix) determining the inner product on 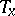 (with respect to the basis
(with respect to the basis 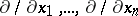 , cf. Tangent vector). Then in local coordinates,
, cf. Tangent vector). Then in local coordinates,
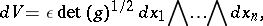 |
where 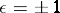 depending on whether the orientation of
depending on whether the orientation of  corresponds to the standard one on
corresponds to the standard one on 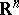 or not (under the given coordinate chart).
or not (under the given coordinate chart).
On a Riemannian manifold  a function
a function  is integrated by intergrating the
is integrated by intergrating the  -form
-form  over
over  in the sense of integration on manifolds.
in the sense of integration on manifolds.
Let  denote the Hodge star operator (cf. Laplace operator). The divergence of a vector field, locally given by
denote the Hodge star operator (cf. Laplace operator). The divergence of a vector field, locally given by 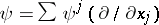 , is defined as the function
, is defined as the function
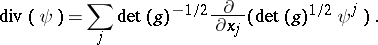 |
One then has
 |
and, on integration over an  -chain in
-chain in 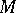 , by the Stokes formula there results the higher-dimensional divergence theorem, which specializes to the usual one for
, by the Stokes formula there results the higher-dimensional divergence theorem, which specializes to the usual one for 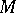 a
a  -dimensional submanifold with boundary in
-dimensional submanifold with boundary in  .
.
References
| [a1] | M. Spivak, "Calculus on manifolds" , Benjamin (1965) |
| [a2] | M. Hazewinkel, "A tutorial introduction to differentiable manifolds and calculus on manifolds" W. Schiehlen (ed.) W. Wedig (ed.) , Analysis and estimation of stochastic mechanical systems , Springer (Wien) (1988) pp. 316–340 |
| [a3] | Y. Choquet-Bruhat, C. DeWitt-Morette, M. Dillard-Bleick, "Analysis, manifolds, and physics" , North-Holland (1977) (Translated from French) |
Volume form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Volume_form&oldid=14716