Volterra series
integro-power series
A series containing the powers of the unknown function under the integral sign. Let  be a continuous function in all variables in a cube
be a continuous function in all variables in a cube  and let
and let  be an arbitrary continuous function on
be an arbitrary continuous function on  . The expression
. The expression
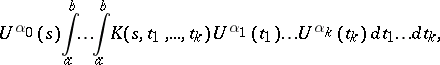 |
where  are non-negative integers and
are non-negative integers and  , is called a Volterra term of degree
, is called a Volterra term of degree  in
in  . Two Volterra terms of degree
. Two Volterra terms of degree 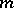 belong to the same type if they differ only in their kernels
belong to the same type if they differ only in their kernels 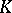 . The finite sum of Volterra terms (of all types) of degree
. The finite sum of Volterra terms (of all types) of degree  is called a Volterra form of degree
is called a Volterra form of degree  in the function
in the function  . It is denoted by
. It is denoted by
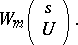 |
Let
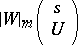 |
denote the Volterra form in which the kernel 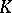 is replaced by
is replaced by 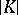 , and let
, and let
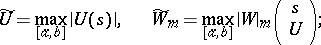 |
then
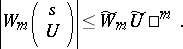 |
The expression
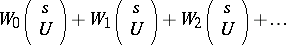 |
is called a Volterra series. If the series of numbers  converges, then the Volterra series is called regularly convergent. In this case the Volterra series converges absolutely and uniformly, and its sum is continuous on
converges, then the Volterra series is called regularly convergent. In this case the Volterra series converges absolutely and uniformly, and its sum is continuous on  .
.
Analogously one introduces Volterra series in several functional arguments, and Volterra series in which  is replaced by some closed bounded set in a finite-dimensional Euclidean space. Volterra series are a particular case of the more general concept of an abstract power series.
is replaced by some closed bounded set in a finite-dimensional Euclidean space. Volterra series are a particular case of the more general concept of an abstract power series.
References
| [1] | A.M. Lyapunov, "On equilibrium figures deviating slightly from ellipsoids of rotation of homogeneous fluid masses" , Collected Works , 4 , Moscow (1959) (In Russian) |
| [2] | E. Schmidt, "Zur Theorie der linearen und nichtlinearen Integralgleichungen III" Math. Ann. , 65 (1908) pp. 370–399 |
| [3] | M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian) |
Comments
A non-linear input-output dynamical system with input  and output
and output  gives rise to a Volterra series of the form
gives rise to a Volterra series of the form
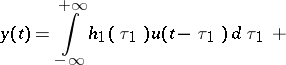 |
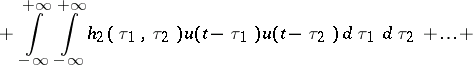 |
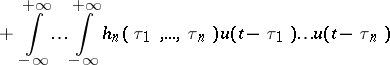 |
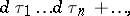 |
in which  if
if 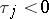 for some
for some  . Such series were first introduced by V. Volterra, [a1], and first applied to questions of system theory by N. Wiener, leading to Wiener integrals, [a2]. Cf. [a3] for an extensive discussion of Volterra series in system theory.
. Such series were first introduced by V. Volterra, [a1], and first applied to questions of system theory by N. Wiener, leading to Wiener integrals, [a2]. Cf. [a3] for an extensive discussion of Volterra series in system theory.
References
| [a1] | V. Volterra, "Theory of functionals and of integral and integro-differential equations" , Dover, reprint (1959) (Translated from French) |
| [a2] | N. Wiener, "Nonlinear problems in random theory" , M.I.T. (1958) |
| [a3] | M. Schetzen, "The Volterra and Wiener theories of nonlinear systems" , Wiley (1980) |
Volterra series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Volterra_series&oldid=11667