Vlasov-Poisson-Fokker-Planck system
The linear Fokker–Planck operator is a model for a certain type of collision in a gas or plasma of particles, which are assumed to be described by a kinetic distribution function  . This means that the number of particles having their positions and velocities
. This means that the number of particles having their positions and velocities  at time
at time  is given by
is given by  . The linear Fokker–Planck collision process has been introduced by S. Chandrasekhar [a6]. The main assumption is that the collisional effects take the form of a stochastic perturbation in Newton's laws of classical mechanics, which are written as
. The linear Fokker–Planck collision process has been introduced by S. Chandrasekhar [a6]. The main assumption is that the collisional effects take the form of a stochastic perturbation in Newton's laws of classical mechanics, which are written as
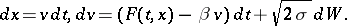 |
Here,  denotes the standard Wiener process,
denotes the standard Wiener process,  is a diffusion coefficient,
is a diffusion coefficient,  is a friction parameter and
is a friction parameter and  is an external force (per mass unit). This random perturbation can be interpreted as the result of interactions with a thermal bath at temperature
is an external force (per mass unit). This random perturbation can be interpreted as the result of interactions with a thermal bath at temperature 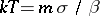 , with
, with 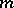 the mass of particles and
the mass of particles and  the Boltzmann constant. Writing the local conservation of the number of particles
the Boltzmann constant. Writing the local conservation of the number of particles 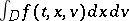 , one obtains the Vlasov–Fokker–Planck equation
, one obtains the Vlasov–Fokker–Planck equation
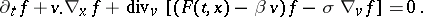 |
The Fokker–Planck term
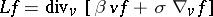 |
can also be viewed as a simplified version of the Fokker–Planck–Landau collision operator, which is quadratic as the Boltzmann collision operator, see [a9] or [a7].
There are two situations where the Vlasov–Fokker–Planck equation is relevant: for charged particles and for gravitational systems. When dealing with a self-consistent force field 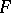 , one obtains in both cases the Poisson equation
, one obtains in both cases the Poisson equation
 |
The constant 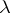 is positive in the Coulombic case and negative in the Newtonian case. See [a8], [a10] for discussions on this model in the latter gravitational case.
is positive in the Coulombic case and negative in the Newtonian case. See [a8], [a10] for discussions on this model in the latter gravitational case.
Concerning the mathematical study of the Vlasov–Poisson–Fokker–Planck system, the situation is comparable with the Vlasov–Poisson system, which is obtained when 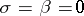 . The main differences are that there are no characteristics, and that the Laplacian term gives rise to smoothing effects. Actually, the Vlasov–Fokker–Planck operator is hypo-elliptic as soon as
. The main differences are that there are no characteristics, and that the Laplacian term gives rise to smoothing effects. Actually, the Vlasov–Fokker–Planck operator is hypo-elliptic as soon as 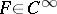 ; when
; when 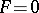 , the Green function can be computed explicitly.
, the Green function can be computed explicitly.
Weak solutions in the whole space  ,
, 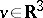 can be obtained exactly as for the Vlasov–Poisson case, using an estimate of the energy
can be obtained exactly as for the Vlasov–Poisson case, using an estimate of the energy
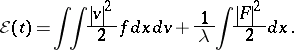 |
Existence of strong solutions (with a bounded force  ) is obtained in [a2], and smoothing effects are provided in [a3]. For a bounded domain
) is obtained in [a2], and smoothing effects are provided in [a3]. For a bounded domain 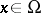 ,
, 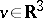 with boundary conditions, existence of weak solutions is obtained in [a5]. Concerning the asymptotics, it is proved in [a4] that
with boundary conditions, existence of weak solutions is obtained in [a5]. Concerning the asymptotics, it is proved in [a4] that  tends to a stationary solution when
tends to a stationary solution when 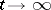 (at least in the Coulombic case), by using the decrease of the free energy
(at least in the Coulombic case), by using the decrease of the free energy
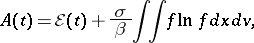 |
which satisfies
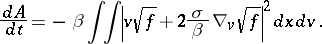 |
The same analysis has been generalized to the case of a bounded domain in [a1].
References
| [a1] | L.L. Bonilla, J.A. Carrillo, J. Soler, "Asymptotic behavior of an initial-boundary value problem for the Vlasov–Poisson–Fokker–Planck system" SIAM J. Appl. Math. , to appear (1997) |
| [a2] | F. Bouchut, "Existence and uniqueness of a global smooth solution for the Vlasov–Poisson–Fokker–Planck system in three dimensions" J. Funct. Anal. , 111 (1993) pp. 239–258 |
| [a3] | F. Bouchut, "Smoothing effect for the non-linear Vlasov–Poisson–Fokker–Planck system" J. Diff. Eq. , 122 (1995) pp. 225–238 |
| [a4] | F. Bouchut, J. Dolbeault, "On long time asymptotics of the Vlasov–Fokker–Planck equation and of the Vlasov–Poisson–Fokker–Planck system with coulombic and newtonian potentials" Diff. Int. Eq. , 8 (1995) pp. 487–514 |
| [a5] | J.A. Carrillo, "Global weak solutions of the absorption and reflection-type initial-boundary value problems for the Vlasov–Poisson–Fokker–Planck system" submitted (1996) |
| [a6] | S. Chandrasekhar, "Stochastic problems in physics and astronomy" Rev. Mod. Phys. , 15 (1943) pp. 1–89 |
| [a7] | S. Chapman, T.G. Cowling, "The mathematical theory of non-uniform gases" , Cambridge Univ. Press (1939) |
| [a8] | M.K.H. Kiesling, "On the equilibrium statistical mechanics of isothermal classical gravitating matter" J. Stat. Phys. , 55 (1989) pp. 203–257 |
| [a9] | E.M. Lifshitz, L.P. Pitaevskii, "Physical kinetics" , Pergamon (1981) |
| [a10] | T. Padmanabhan, "Statistical mechanics of gravitating systems" Phys. Rep. , 188 (1990) pp. 285–362 |
Vlasov-Poisson-Fokker-Planck system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vlasov-Poisson-Fokker-Planck_system&oldid=16992