Vitali-Hahn-Saks theorem
Let 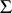 be a
be a 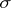 -algebra (cf. also Borel field of sets). Let
-algebra (cf. also Borel field of sets). Let 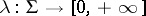 be a non-negative set function and let
be a non-negative set function and let  , where
, where 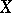 is a normed space. One says that
is a normed space. One says that 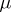 is absolutely continuous with respect to
is absolutely continuous with respect to 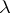 , denoted by
, denoted by 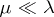 , if for every
, if for every 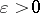 there exists a
there exists a 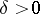 such that
such that 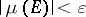 whenever
whenever 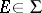 and
and  (cf. also Absolute continuity). A sequence
(cf. also Absolute continuity). A sequence 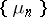 is uniformly absolutely continuous with respect to
is uniformly absolutely continuous with respect to 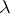 if for every
if for every 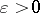 there exists a
there exists a 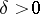 such that
such that 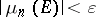 whenever
whenever  ,
, 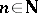 and
and 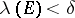 .
.
The Vitali–Hahn–Saks theorem [a7], [a2] says that for any sequence 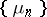 of signed measures
of signed measures 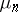 which are absolutely continuous with respect to a measure
which are absolutely continuous with respect to a measure 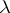 and for which
and for which 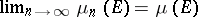 exists for each
exists for each 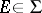 , the following is true:
, the following is true:
i) the limit 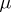 is also absolutely continuous with respect to this measure, i.e.
is also absolutely continuous with respect to this measure, i.e. 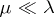 ;
;
ii) 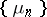 is uniformly absolutely continuous with respect to
is uniformly absolutely continuous with respect to 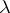 . This theorem is closely related to integration theory [a8], [a3]. Namely, if
. This theorem is closely related to integration theory [a8], [a3]. Namely, if 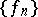 is a sequence of functions from
is a sequence of functions from  , where
, where 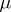 is the Lebesgue measure, and
is the Lebesgue measure, and
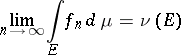 |
exists for each measurable set 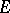 , then the sequence
, then the sequence 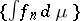 is uniformly absolutely
is uniformly absolutely 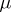 -continuous and
-continuous and  is absolutely
is absolutely 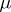 -continuous, [a3].
-continuous, [a3].
R.S. Phillips [a5] and C.E. Rickart [a6] have extended the Vitali–Hahn–Saks theorem to measures with values in a locally convex topological vector space (cf. also Locally convex space).
There are also generalizations to functions defined on orthomodular lattices and with more general properties ([a1], [a4]).
See also Nikodým convergence theorem; Brooks–Jewett theorem.
References
| [a1] | P. Antosik, C. Swartz, "Matrix methods in analysis" , Lecture Notes Math. , 1113 , Springer (1985) |
| [a2] | N. Dunford, J.T. Schwartz, "Linear operators, Part I" , Interscience (1958) |
| [a3] | H. Hahn, "Über Folgen linearer Operationen" Monatsh. Math. Physik , 32 (1922) pp. 3–88 |
| [a4] | E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995) |
| [a5] | R.S. Phillips, "Integration in a convex linear topological space" Trans. Amer. Math. Soc. , 47 (1940) pp. 114–145 |
| [a6] | C.E. Rickart, "Integration in a convex linear topological space" Trans. Amer. Math. Soc. , 52 (1942) pp. 498–521 |
| [a7] | S. Saks, "Addition to the note on some functionals" Trans. Amer. Math. Soc. , 35 (1933) pp. 967–974 |
| [a8] | G. Vitali, "Sull' integrazione per serie" Rend. Circ. Mat. Palermo , 23 (1907) pp. 137–155 |
Vitali-Hahn-Saks theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vitali-Hahn-Saks_theorem&oldid=13281