Vinogradov theorem about the average
From Encyclopedia of Mathematics
A theorem providing an upper bound of the value of a Vinogradov integral:
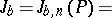 |
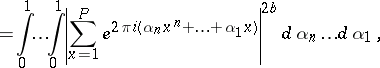 |
where  is the average value of the trigonometric sum. It is formulated as follows. If, for a non-negative integer
is the average value of the trigonometric sum. It is formulated as follows. If, for a non-negative integer  one sets
one sets
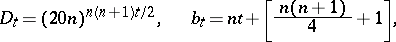 |
then, if  and for an integer
and for an integer  ,
,
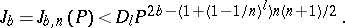 |
The estimate of  given by Vinogradov's theorem is asymptotically exact. The theorem is fundamental in the Vinogradov method for estimating Weyl sums (cf. Weyl sum). In addition, it yielded a number of almost optimal results in classical problems in number theory (cf. Waring problem; Hilbert–Kamke problem; Distribution modulo one of a polynomial).
given by Vinogradov's theorem is asymptotically exact. The theorem is fundamental in the Vinogradov method for estimating Weyl sums (cf. Weyl sum). In addition, it yielded a number of almost optimal results in classical problems in number theory (cf. Waring problem; Hilbert–Kamke problem; Distribution modulo one of a polynomial).
References
| [1] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [2] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
How to Cite This Entry:
Vinogradov theorem about the average. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vinogradov_theorem_about_the_average&oldid=12231
Vinogradov theorem about the average. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vinogradov_theorem_about_the_average&oldid=12231
This article was adapted from an original article by A.A. Karatsuba (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article