Vector tube
A closed set 
of points of a space 
in which there has been specified a vector field 
such that the normal vector 
is orthogonal to 
everywhere on its boundary surface 
. The vector tube 
consists of vector lines 
of the field 
, i.e. curves in 
at each point of which the tangent direction coincides with the direction of 
. A line 
is completely contained in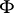 
if one point of 
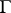is contained in 
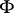. If 
is the field of velocities of a stationary liquid flow, then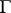 
is the trajectory of the liquid particles, while 
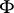is the part of 
"swept along" by the motion of a given amount of liquid particles.
The intensity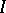 
of the tube 
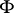in the cross-section 
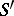is the flux (cf. Vector analysis) of 
across 
:
 |
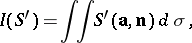where 
is the unit normal vector to 
. If the field 
is solenoidal (
), the law of preservation of the intensity of the vector tube holds:
 |
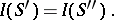Let 
be the orthogonal Cartesian coordinates of the vector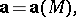 
and let 
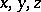be the coordinates of the point 
. Then the boundary of 
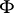is locally defined by an equation 
, where 
satisfies the partial differential equation
 |
 |
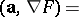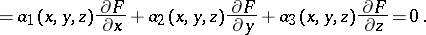Comments
References
| [a1] | A.P. Wills, "Vector analysis with an introduction to tensor analysis" , Dover, reprint (1958) pp. Sect. 45 |
Vector tube. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_tube&oldid=18570