Vector function
A function 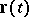 of an argument
of an argument 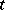 whose values belong to a vector space
whose values belong to a vector space 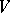 .
.
A vector function with values in a finite-dimensional (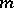 -dimensional) vector space
-dimensional) vector space 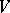 is completely determined by its components
is completely determined by its components 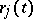 ,
,  , with respect to some basis
, with respect to some basis 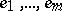 of
of 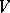 :
:
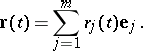 | (1) |
A vector function is said to be continuous, differentiable, etc. (at a point or in a domain) if all functions 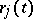 are continuous, differentiable, etc. The following formulas are valid for a function
are continuous, differentiable, etc. The following formulas are valid for a function  of one variable:
of one variable:
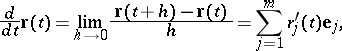 | (2) |
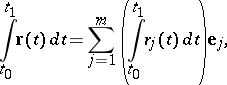 | (3) |
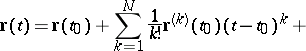 |
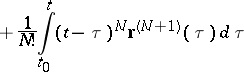 |
(Taylor's formula).
The set of vectors 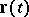 (starting at zero in
(starting at zero in 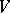 ) is called the hodograph of the vector function. The first derivative
) is called the hodograph of the vector function. The first derivative 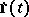 of a vector function of one real variable is a vector in
of a vector function of one real variable is a vector in 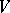 tangent to the hodograph at the point
tangent to the hodograph at the point 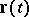 . If
. If  describes the motion of a point mass, where
describes the motion of a point mass, where 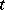 denotes the time, then
denotes the time, then 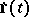 is the instantaneous velocity vector of the point at the time
is the instantaneous velocity vector of the point at the time 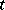 . The second derivative
. The second derivative 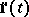 is the acceleration vector of the point.
is the acceleration vector of the point.
Partial derivatives and multiple integrals of vector functions of several variables are defined in analogy with formulas (2) and (3). See Vector analysis; Gradient; Divergence; Curl, for the concepts of vector analysis for vector functions.
In an infinite-dimensional normed vector space with a basis, the representation of a vector function in the form (1) is an infinite series, and a coordinate-wise definition of the operations of mathematical analysis involves difficulties connected with the concepts of convergence of series, the possibility of term-by-term differentiation and integration, etc.
References
| [1] | N.E. Kochin, "Vector calculus and fundamentals of tensor calculus" , Moscow (1965) (In Russian) |
| [2] | P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian) |
Comments
References
| [a1] | R. Courant, F. John, "Introduction to calculus and analysis" , 1 , Wiley (Interscience) (1965) |
| [a2] | J.E. Marsden, A.J. Tromba, "Vector calculus" , Freeman (1981) |
| [a3] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1960) (Translated from French) |
| [a4] | A. Jeffrey, "Mathematics for scientists and engineers" , v. Nostrand-Reinhold (1989) pp. 493ff |
Vector function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_function&oldid=11242