Vector analysis
A branch of vector calculus in which scalar and vector fields are studied (cf. Scalar field; Vector field).
One of the fundamental concepts in vector analysis for the study of scalar fields is the gradient. A scalar field 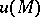 is said to be differentiable at a point
is said to be differentiable at a point 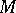 of a domain
of a domain 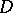 if the increment of the field,
if the increment of the field, 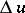 , at
, at 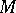 may be written as
may be written as
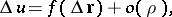 |
where  is the vector connecting the points
is the vector connecting the points 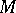 and
and 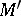 ,
, 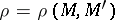 is the distance between
is the distance between 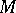 and
and 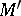 and
and 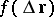 is a linear form applied to the vector
is a linear form applied to the vector  . The linear form
. The linear form 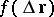 may be uniquely represented as
may be uniquely represented as
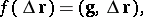 |
where 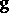 is a vector which does not depend on
is a vector which does not depend on 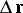 (i.e. on the choice of
(i.e. on the choice of 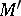 ). The vector
). The vector 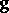 is said to be the gradient of the scalar field and is denoted by the symbol
is said to be the gradient of the scalar field and is denoted by the symbol 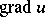 . If the scalar field is differentiable at every point of some domain,
. If the scalar field is differentiable at every point of some domain, 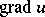 is a vector field. The direction of the gradient is always orthogonal to the level lines (surfaces)
is a vector field. The direction of the gradient is always orthogonal to the level lines (surfaces) 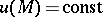 of the scalar field
of the scalar field  , with the directional derivative given by
, with the directional derivative given by
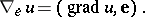 |
The concepts of divergence and curl are also employed in the study of vector fields. Let a vector field 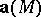 be differentiable at a point
be differentiable at a point 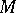 of a certain domain
of a certain domain 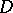 , i.e. the field increment at the point
, i.e. the field increment at the point 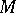 can be uniquely represented as
can be uniquely represented as
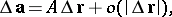 |
where 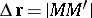 and
and 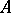 is a linear operator which is independent of
is a linear operator which is independent of 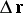 (of the choice of
(of the choice of 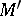 ). The divergence
). The divergence 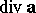 of the vector field
of the vector field 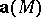 is the following scalar invariant of the linear operator
is the following scalar invariant of the linear operator  :
:
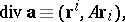 | (*) |
where 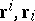 are dual bases:
are dual bases: 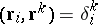 (
(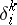 is the Kronecker symbol). If
is the Kronecker symbol). If 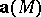 is the velocity field of a stationary flow of a non-compressible liquid,
is the velocity field of a stationary flow of a non-compressible liquid, 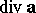 at the point
at the point 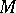 denotes the intensity of the source (
denotes the intensity of the source (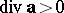 ) or of the sink (
) or of the sink (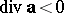 ) present at
) present at 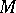 , or their absence (
, or their absence (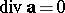 ).
).
The curl (rotor) 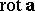 of the vector field
of the vector field 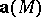 on a domain in
on a domain in 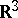 is the following vector invariant of the linear operator
is the following vector invariant of the linear operator 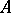 from (*):
from (*):
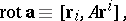 |
where 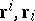 are dual bases. The curl of a vector field may be interpreted as the "rotational component" of this field.
are dual bases. The curl of a vector field may be interpreted as the "rotational component" of this field.
For vector and scalar fields of class 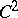 repeated operations are possible, for example:
repeated operations are possible, for example:
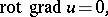 |
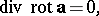 |
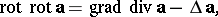 |
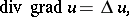 |
where 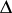 is the Laplace operator.
is the Laplace operator.
Gradient, divergence and curl together are usually known as the basic differential operations of vector analysis. See Curl; Gradient; Divergence for their properties and expressions in special coordinate systems.
Fundamental integral formulas, connecting volume, surface and contour integrals, can be written down in terms of the basic operations of vector analysis. Let a vector field be continuously differentiable in a bounded connected domain 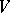 with piecewise-smooth boundary
with piecewise-smooth boundary 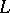 .
.
Let 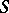 be a bounded, complete, piecewise-smooth, two-sided (oriented) surface with piecewise-smooth boundary
be a bounded, complete, piecewise-smooth, two-sided (oriented) surface with piecewise-smooth boundary  . Then the Stokes formula will be applicable:
. Then the Stokes formula will be applicable:
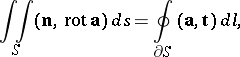 |
where the vector 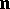 normal to
normal to  and the vector
and the vector 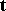 tangent to
tangent to 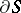 must be determined in accordance with the orientations of the surface
must be determined in accordance with the orientations of the surface 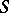 and its boundary
and its boundary 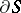 . The integral
. The integral 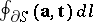 is known as the circulation of
is known as the circulation of  along
along 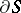 . If the circulation of a vector field along an arbitrary closed piecewise-smooth curve in a given domain is zero, the vector field is said to be potential (or conservative) in this domain. In a simply-connected domain a vector field is conservative if
. If the circulation of a vector field along an arbitrary closed piecewise-smooth curve in a given domain is zero, the vector field is said to be potential (or conservative) in this domain. In a simply-connected domain a vector field is conservative if  . For a conservative vector field there exists the so-called scalar potential, which is a function
. For a conservative vector field there exists the so-called scalar potential, which is a function 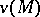 such that
such that 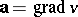 ; here
; here
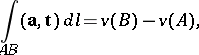 |
where the points 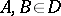 ,
, 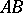 is a piecewise-smooth curve in
is a piecewise-smooth curve in 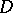 ,
, 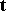 is the unit vector tangent to
is the unit vector tangent to 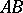 , and
, and 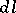 is the line element of
is the line element of 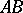 .
.
Let the vector field 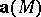 be continuously differentiable in a bounded connected domain
be continuously differentiable in a bounded connected domain 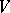 with piecewise-smooth boundary
with piecewise-smooth boundary 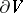 ; the Ostrogradski formula reads as follows:
; the Ostrogradski formula reads as follows:
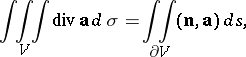 |
where 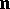 is the exterior normal vector to
is the exterior normal vector to 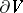 .
.
The integral 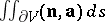 is said to be the flux of
is said to be the flux of 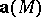 across
across 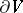 . If the flux of a vector field across an arbitrary, piecewise-smooth, non-self-intersecting, oriented surface in
. If the flux of a vector field across an arbitrary, piecewise-smooth, non-self-intersecting, oriented surface in 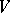 which is the boundary of some bounded subdomain of
which is the boundary of some bounded subdomain of 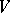 is zero, the vector field
is zero, the vector field 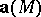 is said to be solenoidal in
is said to be solenoidal in 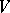 . For a continuously-differentiable vector field to be solenoidal it is necessary and sufficient that
. For a continuously-differentiable vector field to be solenoidal it is necessary and sufficient that 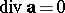 at all points of
at all points of 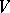 . For a solenoidal vector field
. For a solenoidal vector field 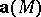 there exists a so-called vector potential: a function
there exists a so-called vector potential: a function 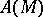 such that
such that
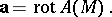 |
If the divergence and the curl of a vector field are defined at each point 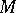 of a simply-connected domain
of a simply-connected domain 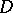 , the vector field can be represented everywhere in
, the vector field can be represented everywhere in 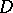 as the sum of a potential field
as the sum of a potential field 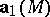 and a solenoidal field
and a solenoidal field 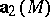 (Helmholtz' theorem):
(Helmholtz' theorem):
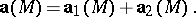 |
Vector fields for which 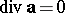 and
and 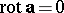 are called harmonic. The potential
are called harmonic. The potential  of a harmonic vector field satisfies the Laplace equation. The scalar field
of a harmonic vector field satisfies the Laplace equation. The scalar field  is also said to be harmonic. For references, see Vector calculus.
is also said to be harmonic. For references, see Vector calculus.
Comments
Ostrogradski's formula is commonly called Gauss' formula.
The condition 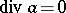 is necessary for a vector field to be solenoidal. It is sufficient on, for example, convex domains. The general additional condition is that the second homology of the domain vanishes. This can easily be seen from the de Rham cohomology theory. There are examples of vector fields on
is necessary for a vector field to be solenoidal. It is sufficient on, for example, convex domains. The general additional condition is that the second homology of the domain vanishes. This can easily be seen from the de Rham cohomology theory. There are examples of vector fields on  -space with one point removed which have vanishing divergence, but are not solenoidal.
-space with one point removed which have vanishing divergence, but are not solenoidal.
The notions of gradient, divergence, Laplace operator, flux of a vector field, and the given integral formulas can easily be extended to higher-dimensional Euclidean spaces and Riemannian manifolds, and all other notions can be extended to Riemannian  -manifolds.
-manifolds.
In this context, the given integral formulas appear in a unified way as Stokes' formula, saying that the integral of a 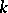 -form over the piecewise-regular boundary of a smooth orientable
-form over the piecewise-regular boundary of a smooth orientable 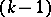 -submanifold is equal to the integral of its exterior differential over the submanifold itself.
-submanifold is equal to the integral of its exterior differential over the submanifold itself.
References
| [a1] | A. Marsden, "Calculus" , 3 , Springer (1988) |
| [a2] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
Vector analysis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_analysis&oldid=16895