Vector
geometric
A directed segment of a straight line in a Euclidean space, one end of which (the point 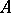 ) is said to be the origin, while the other (the point
) is said to be the origin, while the other (the point 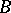 ) is said to be the end of the vector. Such a vector may be denoted by
) is said to be the end of the vector. Such a vector may be denoted by  ,
,  ,
, 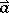 , or
, or 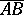 . A vector whose origin and end coincide is said to be a zero vector, and is usually denoted by
. A vector whose origin and end coincide is said to be a zero vector, and is usually denoted by 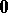 . A vector is characterized by its modulus (or length), which is equal to the length of the segment
. A vector is characterized by its modulus (or length), which is equal to the length of the segment 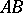 and is denoted by
and is denoted by 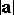 , and by its direction: from
, and by its direction: from 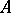 to
to 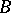 . The vector
. The vector 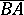 is said to be the vector opposite to
is said to be the vector opposite to 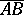 . A vector with length equal to one is called a unit vector. Any direction may be assigned to a zero vector. Two vectors are said to be collinear if they are situated on one straight line or on two parallel lines; they are called coplanar if they lie in the same plane or in two parallel planes. Two collinear vectors are said to be identically (oppositely) directed if their end points are on the same side (on opposite sides) of the straight line connecting their origins, or are on the same side of their common origin. Two vectors
. A vector with length equal to one is called a unit vector. Any direction may be assigned to a zero vector. Two vectors are said to be collinear if they are situated on one straight line or on two parallel lines; they are called coplanar if they lie in the same plane or in two parallel planes. Two collinear vectors are said to be identically (oppositely) directed if their end points are on the same side (on opposite sides) of the straight line connecting their origins, or are on the same side of their common origin. Two vectors 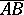 and
and 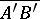 on the same straight line are said to be identically (oppositely) directed if one of the rays
on the same straight line are said to be identically (oppositely) directed if one of the rays 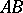 ,
, 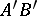 is (is not) totally included in the other. Two vectors are said to be equal if they have equal moduli and are identically directed (such vectors are also known as free vectors). All zero vectors are said to be equal.
is (is not) totally included in the other. Two vectors are said to be equal if they have equal moduli and are identically directed (such vectors are also known as free vectors). All zero vectors are said to be equal.
In addition to free vectors, i.e. vectors whose origin is immaterial, vectors characterized by their length, direction and the location of their origin (the point of application) are often considered in mechanics and physics. A class of equal vectors lying on the same straight line is said to be a sliding vector. One also considers bound vectors, which are said to be equal if they have not only equal moduli and identical directions, but also a common point of application. Vector calculus, which is the study of operations performed on vectors, is based on free vectors, since two given free vectors are equivalent to a given sliding vector or a given bound vector.
The concept of a vector arose as a mathematical abstraction of objects which are characterized by magnitude and direction, such as displacement, velocity and magnetic or electric field strength.
The concept of a vector may be introduced axiomatically (cf. Vector space).
Comments
A geometric vector as defined above comes from such concepts as a force in mechanics, a quantity that has magnitude, direction and a point of application. A mathematical setting is that of an affine space, which is a vector space "up to the location of its origin" or, more precisely, a simply transitive group action 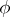 of (the underlying additive group of) a vector space
of (the underlying additive group of) a vector space 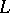 on a set
on a set 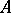 . The simple transitivity defines a mapping
. The simple transitivity defines a mapping 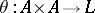 characterized by
characterized by 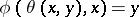 . Writing
. Writing 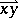 for
for  ,
, 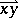 is the free vector defined by the bound vector, or geometric vector,
is the free vector defined by the bound vector, or geometric vector, 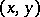 or
or 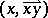 (which has point of application
(which has point of application  and direction and magnitude given by
and direction and magnitude given by 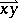 ). For three points
). For three points 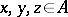 one has
one has 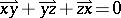 in
in 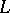 , which is called the Chasles relation (cf. [a1] and Affine space).
, which is called the Chasles relation (cf. [a1] and Affine space).
The displacement law in mechanics says that a force acting on a rigid body can be displaced along its line of action to any new point of application. Thus, a force acting on a rigid body is a sliding vector.
References
| [a1] | M. Berger, "Geometry" , I , Springer (1987) pp. Chapt. 2 |
| [a2] | H. Ziegler, "Mechanics" , I , Addison-Wesley (1965) |
Vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector&oldid=14349