Variety of universal algebras
A class of universal algebras (cf. Universal algebra) defined by a system of identities (cf. Algebraic systems, variety of). A variety of universal algebras may be characterized as a non-empty class of algebras closed under taking quotient algebras, subalgebras and direct products. The last two conditions may be replaced by the requirement of closure under subdirect products. A variety of universal algebras is said to be trivial if it consists of one-element algebras. Every non-trivial variety of universal algebras contains a free algebra with basis of any cardinality. If 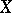 and
and 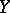 are bases of the same free algebra in a non-trivial variety and
are bases of the same free algebra in a non-trivial variety and 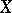 is infinite, then
is infinite, then 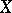 and
and 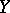 are equipotent. The requirement that one of the bases be infinite is essential, but it may be omitted if the variety contains a finite algebra with more than one element.
are equipotent. The requirement that one of the bases be infinite is essential, but it may be omitted if the variety contains a finite algebra with more than one element.
The variety of universal algebras generated by a class 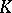 consists of all quotient algebras of subdirect products of algebras in
consists of all quotient algebras of subdirect products of algebras in 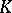 . If a variety of universal algebras is generated by finite algebras, then every finitely-generated algebra in the variety is finite. The congruences of any algebra in a variety of universal algebras
. If a variety of universal algebras is generated by finite algebras, then every finitely-generated algebra in the variety is finite. The congruences of any algebra in a variety of universal algebras  of signature
of signature  commute if and only if there exists a ternary term
commute if and only if there exists a ternary term 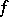 of the signature
of the signature  such that
such that
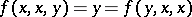 |
for all algebras in  . In similar fashion one can characterize varieties of universal algebras whose algebras have modular or distributive congruence lattices (cf. [1]–[4], [7], [9], [10]).
. In similar fashion one can characterize varieties of universal algebras whose algebras have modular or distributive congruence lattices (cf. [1]–[4], [7], [9], [10]).
In a variety  , an
, an  -ary operation
-ary operation 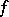 is called trivial if for every algebra in
is called trivial if for every algebra in 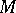 the identity
the identity 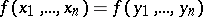 holds. E.g. in the variety of rings with zero multiplication the operation of multiplication is trivial. Every trivial operation
holds. E.g. in the variety of rings with zero multiplication the operation of multiplication is trivial. Every trivial operation 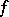 may be replaced by the
may be replaced by the  -ary operation
-ary operation 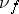 defined by the equation
defined by the equation 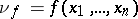 . Suppose that the signatures
. Suppose that the signatures  ,
,  of two varieties of universal algebras
of two varieties of universal algebras 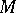 ,
,  , respectively, do not contain trivial operations. A mapping
, respectively, do not contain trivial operations. A mapping 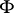 from
from  into the set
into the set 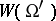 of terms of
of terms of 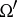 is called admissible if the arities of
is called admissible if the arities of 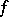 and
and 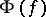 coincide for all
coincide for all 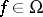 . An admissible mapping
. An admissible mapping 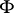 can be extended to a mapping from
can be extended to a mapping from 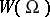 to
to 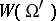 , still denoted by
, still denoted by 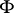 , in a natural fashion. The varieties
, in a natural fashion. The varieties 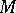 and
and 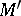 are said to be rationally equivalent if there exist admissible mappings
are said to be rationally equivalent if there exist admissible mappings 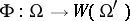 and
and 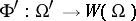 such that
such that 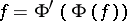 for all
for all 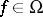 ,
, 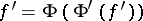 for all
for all 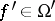 , and if for every defining identity
, and if for every defining identity  (respectively,
(respectively, 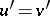 ) of
) of 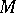 (respectively,
(respectively, 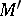 ) the identity
) the identity 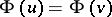 (respectively,
(respectively, 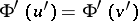 ) holds for all algebras in
) holds for all algebras in 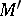 (in
(in 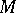 ). The last requirement is equivalent to the fact that every algebra
). The last requirement is equivalent to the fact that every algebra 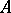 in
in 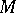 (
(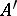 in
in 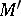 ) corresponds to an algebra in
) corresponds to an algebra in 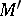 (in
(in 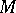 ), where each
), where each  -ary operation
-ary operation 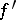 in
in 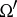 (
(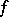 in
in  ) is defined by the equation
) is defined by the equation 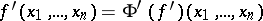 (respectively,
(respectively, 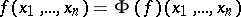 ). The variety of Boolean rings and that of Boolean algebras (cf. Boolean algebra) are rationally equivalent. The variety of unary algebras (cf. Unary algebra) of signature
). The variety of Boolean rings and that of Boolean algebras (cf. Boolean algebra) are rationally equivalent. The variety of unary algebras (cf. Unary algebra) of signature  , with defining identities
, with defining identities
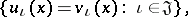 |
is rationally equivalent to the variety of all left 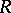 -polygons (cf. Polygon (over a monoid)), where
-polygons (cf. Polygon (over a monoid)), where 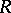 is the quotient monoid of the free monoid generated by
is the quotient monoid of the free monoid generated by  by the congruence generated by the pairs
by the congruence generated by the pairs 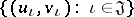 . A variety of universal algebras
. A variety of universal algebras 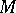 is rationally equivalent to the variety of all right modules over some associative ring if and only if the congruences on any algebra in
is rationally equivalent to the variety of all right modules over some associative ring if and only if the congruences on any algebra in 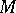 commute, if finite free products (cf. Free product) in
commute, if finite free products (cf. Free product) in 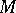 coincide with direct products (cf. Direct product) and if there exist
coincide with direct products (cf. Direct product) and if there exist  -ary derived operations forming a distinguished subalgebra. The first two conditions may be replaced by the requirement: Every subalgebra of any algebra in
-ary derived operations forming a distinguished subalgebra. The first two conditions may be replaced by the requirement: Every subalgebra of any algebra in 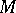 is the class of a certain congruence and every congruence of any algebra in
is the class of a certain congruence and every congruence of any algebra in 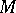 is uniquely determined by the class formed by the subalgebra, [3], [5]–[7].
is uniquely determined by the class formed by the subalgebra, [3], [5]–[7].
The variety of lattices generated by the congruence lattices of all algebras of a certain variety of universal algebras is called a congruence variety. Not every variety of lattices is a congruence variety. There exist congruence varieties which are not modular and differ from the variety of all lattices [7], [8].
References
| [1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [2] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [3] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
| [4] | L.A. Skornyakov, "Elements of general algebra" , Moscow (1983) (In Russian) |
| [5] | B. Csakany, "Primitive classes of algebras which are equivalent to classes of semimodules and modules" Acta Scient. Math. , 24 : 1–2 (1963) pp. 157–164 (In Russian) |
| [6] | B. Csakany, "Abelian properties of primitive classes of universal algebras" Acta Scient. Math. , 25 : 3–4 (1964) pp. 202–208 (In Russian) |
| [7] | G. Grätzer, "Universal algebra" , Springer (1979) |
| [8] | B. Jónsson, "Varieties of lattices: some open problems" B. Csákány (ed.) E. Fried (ed.) E.T. Schmidt (ed.) , Universal Algebra (Esztergom, 1977) , Coll. Math. Soc. J. Bolyai , 29 , North-Holland (1982) pp. 421–436 |
| [9] | J.D.H. Smith, "Mal'cev varieties" , Springer (1976) |
| [10] | W. Taylor, "Characterizing Mal'cev conditions" Algebra Universalis , 3 : 3 (1973) pp. 351–397 |
Comments
The term "variety of universal algebras" is also used for the category formed by all the algebras in a given variety (in the sense defined above) and all the homomorphisms between them; for algebras in a given signature  , these are exactly the varieties in the category of all
, these are exactly the varieties in the category of all  -algebras (cf. Variety in a category). The categories which occur as varieties may be characterized as those equipped with a forgetful functor to the category of sets which is monadic (cf. Triple) and preserves filtered colimits [a1], [a2].
-algebras (cf. Variety in a category). The categories which occur as varieties may be characterized as those equipped with a forgetful functor to the category of sets which is monadic (cf. Triple) and preserves filtered colimits [a1], [a2].
Two varieties are called Morita equivalent if they are equivalent as (abstract) categories; this generalizes the notion of Morita equivalence for rings. Two varieties are equivalent as concrete categories (that is, there is an equivalence between them which reduces to the identity functor on underlying sets) if and only if they are rationally equivalent, as defined above. Many properties of varieties which are invariant within rational equivalence turn out to be definable in categorical terms. For example, varieties of unary algebras are exactly those for which the underlying-set functor preserves coproducts, and varieties rationally equivalent to varieties of modules are exactly those which are Abelian categories (cf. Abelian category). Note that the second of these classes of varieties is closed under Morita equivalence, although the first is not. Any property of varieties which is expressible in terms of subalgebra lattices or congruence lattices will automatically be invariant within Morita equivalence.
In the opposite direction, one can seek syntactic conditions (that is, conditions on the operations and the equations they satisfy) which correspond to familiar categorical properties of a variety. For example, such characterizations have been given [a3] of those varieties which are Cartesian-closed categories and those which are topoi (cf. Topos).
The first volume of an authoritative treatment on universal algebra has appeared [a5]. The topic of Mal'tsev operations (ternary operations 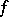 satisfying
satisfying 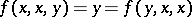 ) has been vigorously pursued recently (1991); an exposition of work up to 1989, mainly due to E. Faro and J. Lambek, is in [a6]. (Cf. Mal'tsev product.)
) has been vigorously pursued recently (1991); an exposition of work up to 1989, mainly due to E. Faro and J. Lambek, is in [a6]. (Cf. Mal'tsev product.)
References
| [a1] | E.G. Manes, "Algebraic theories" , Springer (1976) |
| [a2] | G.C. Wraith, "Algebraic theories" , Lect. notes series , 22 , Aarhus Univ. (1975) |
| [a3] | P.T. Johnstone, "Collapsed toposes and cartesian closed varieties" J. Algebra , 129 (1990) pp. 446–480 |
| [a4] | R. Freese, R. McKenzie, "Commutator theory for congruence modular varieties" , Cambridge Univ. Press (1987) |
| [a5] | W. Taylor, "Algebras, lattices, varieties" , 1 , Wadsworth (1987) |
| [a6] | A.M. San Luis Fernandez, "Sobre teorías algebraicas con una operación de Malcev" Alxebra , 55 (1989) |
Variety of universal algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variety_of_universal_algebras&oldid=16722