Variational series
series of order statistics
An arrangement of the values of a random sample 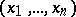 with distribution function
with distribution function 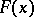 in ascending sequence
in ascending sequence 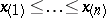 . The series is used to construct the empirical distribution function
. The series is used to construct the empirical distribution function 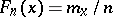 , where
, where 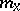 is the number of terms of the series which are smaller than
is the number of terms of the series which are smaller than  . Important characteristics of series of order statistics are its extremal terms (
. Important characteristics of series of order statistics are its extremal terms (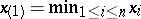 ,
, 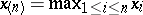 ) and the range
) and the range 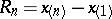 . The densities of the distributions of the minimum and maximum terms of a series of order statistics in the case
. The densities of the distributions of the minimum and maximum terms of a series of order statistics in the case
 |
are defined by the expressions
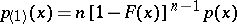 |
and
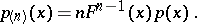 |
Considered as a stochastic process with time index 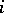 ,
, 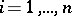 , the series of order statistics forms a non-homogeneous Markov chain.
, the series of order statistics forms a non-homogeneous Markov chain.
References
| [1] | S.S. Wilks, "Mathematical statistics" , Wiley (1962) |
Comments
The phrase "variational series" is almost never used in the West. Cf. also Order statistic.
References
| [a1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Variational series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variational_series&oldid=14157