Variation of a set
A number characterizing the 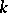 -dimensional content of a set in
-dimensional content of a set in  -dimensional Euclidean space. The zero variation
-dimensional Euclidean space. The zero variation 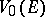 of a closed bounded set
of a closed bounded set 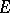 is the number of components of this set.
is the number of components of this set.
In the simplest case of the plane, the linear variation of a set 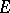 (i.e. the first-order variation of
(i.e. the first-order variation of 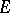 ) is the integral
) is the integral
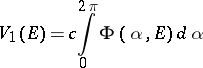 |
of the function
 |
where the integration is performed over the straight line 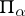 passing through the coordinate origin,
passing through the coordinate origin, 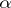 is the angle formed by
is the angle formed by 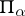 with a given axis and
with a given axis and 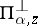 is the straight line normal to
is the straight line normal to 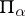 which intersects it at the point
which intersects it at the point  . The normalizing constant
. The normalizing constant  is so chosen that the variation
is so chosen that the variation 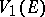 of an interval
of an interval 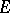 is equal to its length. For sufficiently simple sets, e.g. for rectifiable curves, the variation of the set is equal to the length of the curve. For a closed domain
is equal to its length. For sufficiently simple sets, e.g. for rectifiable curves, the variation of the set is equal to the length of the curve. For a closed domain 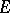 with a rectifiable boundary
with a rectifiable boundary 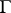 its linear variation
its linear variation 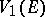 is equal to one-half the length of
is equal to one-half the length of 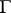 . The second variation of
. The second variation of 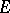 (i.e. the second-order variation of
(i.e. the second-order variation of 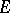 ) is the two-dimensional measure of
) is the two-dimensional measure of 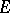 , and
, and 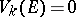 if
if 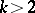 .
.
In  -dimensional Euclidean space the variation
-dimensional Euclidean space the variation 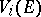 of order
of order 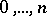 , of a bounded closed set
, of a bounded closed set 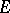 is the integral
is the integral
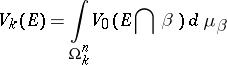 |
of the zero variation of the intersection of 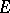 with an
with an 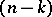 -dimensional plane
-dimensional plane 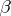 in the space
in the space 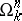 of all
of all 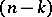 -dimensional planes of
-dimensional planes of 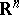 with respect to the Haar measure
with respect to the Haar measure 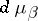 ; normalized so that the
; normalized so that the 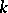 -dimensional unit cube
-dimensional unit cube 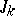 has variation
has variation 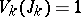 .
.
The variation 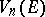 is identical with the
is identical with the  -dimensional Lebesgue measure of the set
-dimensional Lebesgue measure of the set 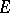 . For convex bodies the (suitably normalized) set variations are identical with Minkowski's mixed volumes (cf. Mixed-volume theory) [4].
. For convex bodies the (suitably normalized) set variations are identical with Minkowski's mixed volumes (cf. Mixed-volume theory) [4].
Properties of the variations of a set.
1) The variations 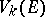 for
for 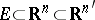 calculated for
calculated for 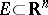 and for
and for 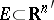 have the same value.
have the same value.
2) The variations of a set can be inductively expressed by the formula
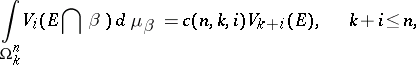 |
where 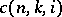 is the normalization constant.
is the normalization constant.
3) 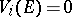 implies
implies 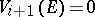 .
.
4) In a certain sense, the variations of a set are not dependent, i.e. for any sequence of numbers  , where
, where 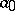 is a positive integer,
is a positive integer, 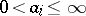 (
(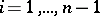 ),
), 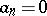 , it is possible to construct a set
, it is possible to construct a set 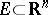 for which
for which 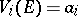 ,
, 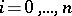 .
.
5) If 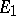 and
and 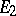 do not intersect,
do not intersect,  . In the general case,
. In the general case,
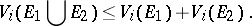 |
For  the variations
the variations 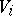 are not monotone, i.e. it can happen for
are not monotone, i.e. it can happen for 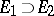 that
that 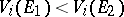 .
.
6) The variations of a set are semi-continuous, i.e. if a sequence of closed bounded sets 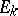 converges (in the sense of deviation in metric) to a set
converges (in the sense of deviation in metric) to a set 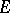 , then
, then
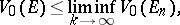 |
and if, in addition, the sums 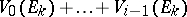 are uniformly bounded, then
are uniformly bounded, then
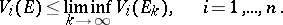 |
7) The variation 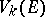 becomes identical with the
becomes identical with the 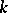 -dimensional Hausdorff measure if
-dimensional Hausdorff measure if 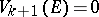 and if
and if
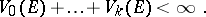 |
These conditions are met, for example, by twice-differentiable manifolds.
The concept of the variation of a set arose in the context of solutions of the Cauchy–Riemann system, and its ultimate formulation is due to A.G. Vitushkin. The set variations proved to be a useful tool in solving certain problems in analysis, in particular that of superposition of functions of several variables [1], and also in approximation problems [2].
References
| [1] | A.G. Vitushkin, "On higher-dimensional variations" , Moscow (1955) (In Russian) |
| [2] | A.G. Vitushkin, "Estimation of the complexity of the tabulation problem" , Moscow (1959) (In Russian) |
| [3] | A.G. Vitushkin, "Proof of the upper semicontinuity of a set variation" Soviet Math. Dokl. , 7 : 1 (1966) pp. 206–209 Dokl. Akad. Nauk SSSR , 166 : 5 (1966) pp. 1022–1025 |
| [4] | A.M. Leontovich, M.S. Mel'nikov, "On the boundedness of the variations of a manifold" Trans. Moscow Math Soc. , 14 (1965) pp. 333–368 Trudy Moskov. Mat. Obshch. , 14 (1965) pp. 306–337 |
| [5] | L.D. Ivanov, "Geometric properties of sets with finite variation" Math. USSR-Sb. , 1 : 2 (1967) pp. 405–427 Mat. Sb. , 72 (114) : 3 (1967) pp. 445–470 |
| [6] | L.D. Ivanov, "On the local structure of sets with finite variation" Math. USSR-Sb. , 7 : 1 (1969) pp. 79–93 Mat. Sb. , 78 (120) : 1 (1969) pp. 85–100 |
Comments
Cf. also Content and Variation of a function.
Variation of a set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variation_of_a_set&oldid=15814