Variation of a function
A numerical characteristic of functions of one real variable which is connected with differentiability properties.
1) Let 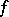 be a complex-valued function defined on an interval
be a complex-valued function defined on an interval 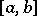 ; its variation
; its variation 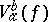 is the least upper bound of sums of the type
is the least upper bound of sums of the type
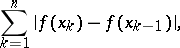 |
where  is an arbitrary system of points on
is an arbitrary system of points on 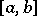 . This definition was given by C. Jordan [1]. If
. This definition was given by C. Jordan [1]. If 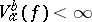 , one says that
, one says that 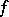 has (is of) bounded (finite) variation over
has (is of) bounded (finite) variation over 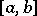 , and the class of all such functions is denoted by
, and the class of all such functions is denoted by 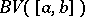 . A real-valued function
. A real-valued function 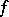 belongs to the class
belongs to the class 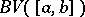 if and only if it can be represented in the form
if and only if it can be represented in the form  , where
, where 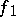 and
and 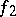 are functions which increase on
are functions which increase on 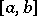 (the Jordan decomposition of functions of bounded variation). The sum, the difference and the product of two functions of class
(the Jordan decomposition of functions of bounded variation). The sum, the difference and the product of two functions of class 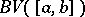 are also functions of class
are also functions of class 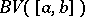 . This is also true of the quotient of two functions of class
. This is also true of the quotient of two functions of class 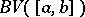 if the modulus of the denominator is larger than a positive constant on
if the modulus of the denominator is larger than a positive constant on 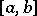 . Every function in
. Every function in 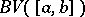 is bounded and cannot have more than a countable set of discontinuity points, all of which are of the first kind. All these properties of functions in
is bounded and cannot have more than a countable set of discontinuity points, all of which are of the first kind. All these properties of functions in 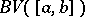 were established by Jordan [1] (see also [2]).
were established by Jordan [1] (see also [2]).
Functions 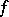 in
in  are almost-everywhere differentiable on
are almost-everywhere differentiable on  and may be represented as
and may be represented as
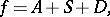 |
where 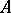 is an absolutely continuous function,
is an absolutely continuous function, 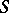 is a singular function and
is a singular function and 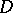 is a saltus function (the Lebesgue decomposition of a function of bounded variation). Such a decomposition is unique if
is a saltus function (the Lebesgue decomposition of a function of bounded variation). Such a decomposition is unique if 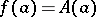 [3], [2].
[3], [2].
The class 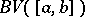 was originally introduced by Jordan in the context of the generalization of the Dirichlet criterion for the convergence of Fourier series of piecewise-monotone functions. It was shown by him that Fourier series of
was originally introduced by Jordan in the context of the generalization of the Dirichlet criterion for the convergence of Fourier series of piecewise-monotone functions. It was shown by him that Fourier series of 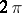 -periodic functions in the class
-periodic functions in the class 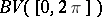 converge at all points of the real axis. Functions of bounded variation subsequently found extensive application in various branches of mathematics, especially in the theory of the Stieltjes integral.
converge at all points of the real axis. Functions of bounded variation subsequently found extensive application in various branches of mathematics, especially in the theory of the Stieltjes integral.
One sometimes also considers classes 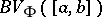 , defined as follows. Let
, defined as follows. Let 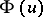 (
(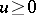 ,
, 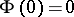 ) be a continuous function which increases monotonically if
) be a continuous function which increases monotonically if 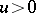 . Let
. Let 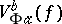 be the least upper bound of sums of the type
be the least upper bound of sums of the type
 |
where 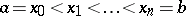 is an arbitrary system of points in
is an arbitrary system of points in 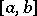 . The quantity
. The quantity 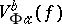 is called the
is called the 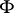 -variation of
-variation of 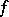 on
on 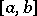 . If
. If 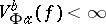 , one says that
, one says that 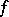 has bounded
has bounded 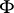 -variation on
-variation on 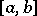 , while the class of such functions is denoted by
, while the class of such functions is denoted by 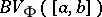 ([4]). If
([4]). If 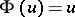 , one obtains Jordan's class
, one obtains Jordan's class 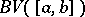 , while if
, while if 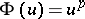 ,
, 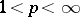 , one obtains Wiener's classes
, one obtains Wiener's classes 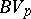 [5]. The definition of the class
[5]. The definition of the class 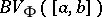 was proposed by L.C. Young [6].
was proposed by L.C. Young [6].
If
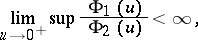 |
then
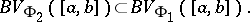 |
In particular, on any interval 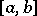 ,
,
 |
for 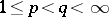 ,
, 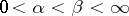 , these being proper inclusions.
, these being proper inclusions.
References
| [1] | C. Jordan, "Sur la série de Fourier" C.R. Acad. Sci. Paris Sér. I Math. , 92 : 5 (1881) pp. 228–230 |
| [2] | I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) |
| [3] | H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) |
| [4] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [5] | N. Wiener, "The quadratic variation of a function and its Fourier coefficients" J. Math. and Phys. , 3 (1924) pp. 72–94 |
| [6] | L.C. Young, "Sur une généralisation de la notion de variation de puissance 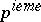 borneé au sens de M. Wiener, et sur la convergence des series de Fourier" C.R. Acad. Sci. Paris Sér. I Math. , 204 (1937) pp. 470–472 borneé au sens de M. Wiener, et sur la convergence des series de Fourier" C.R. Acad. Sci. Paris Sér. I Math. , 204 (1937) pp. 470–472 |
Comments
The variation of a function as defined above is often called the total variation. It is the sum of the negative and positive variations (cf. Negative variation of a function; Positive variation of a function). One has
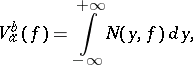 |
where 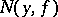 is the Banach indicatrix of
is the Banach indicatrix of 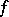 . If
. If 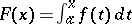 , then
, then
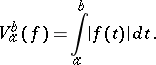 |
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) pp. 266; 270; 272 |
| [a2] | S. Saks, "Theory of the integral" , Hafner (1937) (Translated from French) |
Several different definitions of variation exist for functions of several variables (Arzelà variation; Vitali variation; Pierpont variation; Tonelli plane variation; Fréchet variation; Hardy variation). The following definition, [1], based on the use of the Banach indicatrix, also proved very fruitful. Let a real-valued function 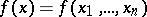 be given and be Lebesgue-measurable on an
be given and be Lebesgue-measurable on an  -dimensional cube
-dimensional cube 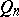 . The variation
. The variation 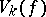 of order
of order 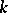 , where
, where 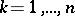 , of
, of 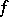 on
on 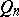 is the number
is the number
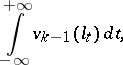 |
where 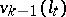 denotes the
denotes the 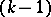 -th variation of the set
-th variation of the set 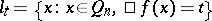 (cf. Variation of a set), while the integral is understood in the sense of Lebesgue. This definition allows one to transfer many properties of functions of bounded variation in one variable to functions of several variables. For instance,
(cf. Variation of a set), while the integral is understood in the sense of Lebesgue. This definition allows one to transfer many properties of functions of bounded variation in one variable to functions of several variables. For instance,
a) 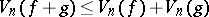 ;
;
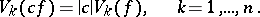 |
b) If a sequence of functions 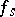 ,
, 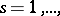 converges uniformly to
converges uniformly to 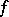 in
in 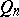 , then
, then
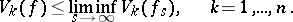 |
c) If the function 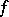 is continuous in
is continuous in 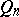 and all its variations are finite,
and all its variations are finite, 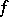 has a total differential almost-everywhere.
has a total differential almost-everywhere.
d) If the function 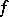 is absolutely continuous in
is absolutely continuous in 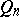 , then
, then
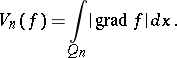 |
e) If the function 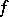 is continuous in a cube
is continuous in a cube 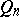 with side-length
with side-length 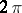 , if it has bounded variations of all orders in
, if it has bounded variations of all orders in 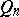 and if it can be periodically extended with period
and if it can be periodically extended with period 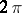 for all arguments
for all arguments  ,
, 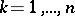 , in the
, in the  -dimensional space, then its Fourier series converges uniformly to it on
-dimensional space, then its Fourier series converges uniformly to it on 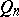 (Pringsheim's theorem).
(Pringsheim's theorem).
A sufficient condition for being of bounded variation is: If the function  has continuous derivatives of all orders up to and including
has continuous derivatives of all orders up to and including 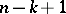 in the cube
in the cube 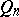 , then its variation of order
, then its variation of order 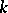 is finite. This theorem is a final theorem in the sense that the smoothness conditions cannot be improved for any
is finite. This theorem is a final theorem in the sense that the smoothness conditions cannot be improved for any 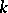 .
.
References
| [1] | A.G. Vitushkin, "On higher-dimensional variations" , Moscow (1955) (In Russian) |
A.G. Vitushkin
Variation of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variation_of_a_function&oldid=18738