Variable-directions method
An iterative method (cf. Iteration methods) for solving systems of linear or non-linear equations arising in difference or projection-difference methods for the approximate solution of, for example, boundary value problems for partial differential equations of elliptic type.
Let, for example, there be two spatial variables and a sequence of square grids 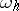 with step
with step 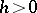 and nodes
and nodes 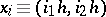 , where
, where 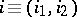 is a vector with integer components. Let
is a vector with integer components. Let 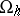 be the set of nodes
be the set of nodes 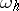 at which one seeks a solution to a difference or projection-difference problem written in the form of the operator equation
at which one seeks a solution to a difference or projection-difference problem written in the form of the operator equation
 |
in the Euclidean space 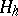 . The latter can be identified with the space of functions given at the nodes of
. The latter can be identified with the space of functions given at the nodes of 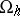 ; the dimension of
; the dimension of 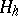 coincides with the number of points
coincides with the number of points 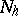 from
from 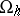 .
.
Let
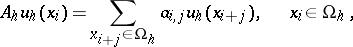 | (1) |
be linear operators mapping 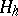 into
into 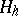 . Among the operators (1) there are such for which the non-zero coefficients
. Among the operators (1) there are such for which the non-zero coefficients 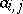 in (1) correspond only to shift vectors
in (1) correspond only to shift vectors 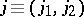 having
having 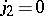 . Such operators are called one-dimensional, acting with respect to
. Such operators are called one-dimensional, acting with respect to 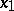 , and they are denoted by
, and they are denoted by 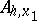 ; similarly, for shift vectors having
; similarly, for shift vectors having 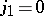 , one defines the one-dimensional operators
, one defines the one-dimensional operators 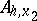 acting on
acting on 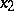 .
.
The systems of equations
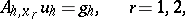 |
split up into individual subsystems, each of which links only the values of  at nodes lying on separate horizontal (for
at nodes lying on separate horizontal (for 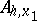 ) or vertical (for
) or vertical (for 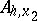 ) lines in the grid. The method is characterized by the use of intertwining operators for
) lines in the grid. The method is characterized by the use of intertwining operators for 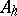 of the form
of the form
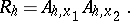 |
The solution to the system
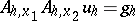 | (2) |
then amounts to the successive solution of the two systems
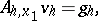 | (3) |
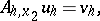 | (4) |
in which one first solves the separate subsystems on the horizontal lines in the grid (in the case (3)) and then varies the directions and solves the subsystems on the vertical lines (in the case (4)). Usually, the operators 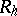 are taken such that only
are taken such that only 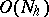 arithmetic operations are involved in solving (3) and (4), and consequently also (2). Therefore, each iteration in the method, of the form
arithmetic operations are involved in solving (3) and (4), and consequently also (2). Therefore, each iteration in the method, of the form
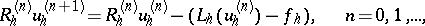 | (5) |
requires 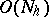 arithmetic operations, where the superscript
arithmetic operations, where the superscript  corresponds to the number of the iteration.
corresponds to the number of the iteration.
The most effective results are obtained for the commutative case, where 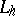 is a self-adjoint positive-definite operator, while the operators
is a self-adjoint positive-definite operator, while the operators 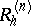 are self-adjoint and commute with
are self-adjoint and commute with 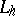 . In that case, for any
. In that case, for any 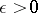 the error in the initial approximation can be reduced in norm by a factor
the error in the initial approximation can be reduced in norm by a factor 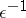 in
in  iterations. The commutative case will be encountered only for boundary value problems in which the variables can be separated, and therefore, the region should be a rectangle. The most common case of the method (5) for the equation
iterations. The commutative case will be encountered only for boundary value problems in which the variables can be separated, and therefore, the region should be a rectangle. The most common case of the method (5) for the equation
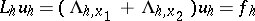 |
is the method
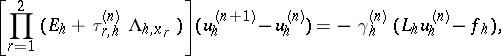 |
where 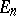 is the identity operator.
is the identity operator.
One also uses approaches based on different variational principles, supplementing the approach in which the iteration parameters are chosen to minimize the norm of the operator for passing from the zero-th iteration to an iteration of a given index.
The method is frequently used as an internal iterative process in two-step iteration methods based on operators that are equivalent in spectrum and suitable for use with variable coefficients and non-linear problems.
References
| [1] | D.W. Peaceman, H.H. Rachford, "The numerical solution of parabolic and elliptic differential equations" SIAM J. , 3 : 1 (1955) pp. 28–41 |
| [2] | E.G. D'yakonov, "Iterative methods for solving difference analogues of boundary value problems for equations of elliptic type" , Kiev (1970) (In Russian) |
| [3] | N.N. Yanenko, "The method of fractional steps; the solution of problems of mathematical physics in several variables" , Springer (1971) (Translated from Russian) |
| [4] | A.A. Samarskii, "Theorie der Differenzverfahren" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1984) (Translated from Russian) |
| [5] | G.I. Marchuk, "Methods of numerical mathematics" , Springer (1982) (Translated from Russian) |
Variable-directions method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variable-directions_method&oldid=11482