Vapnik-Chervonenkis dimension
Vapnik–Červonenkis dimension, VC-dimension
Let 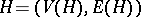 be a hypergraph. The Vapnik–Chervonenkis dimension of
be a hypergraph. The Vapnik–Chervonenkis dimension of 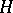 is the largest cardinality of a subset
is the largest cardinality of a subset 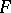 of
of 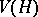 that is scattered by
that is scattered by 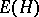 , i.e. such that for all
, i.e. such that for all 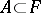 there is an
there is an 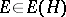 with
with 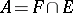 . Thus, it is the same as the index of a Vapnik–Chervonenkis class. It is usually denoted by
. Thus, it is the same as the index of a Vapnik–Chervonenkis class. It is usually denoted by 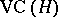 .
.
Computing the Vapnik–Chervonenkis dimension is 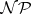 -hard (cf. also
-hard (cf. also 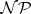 ) for many classes of hypergraphs, [a1], [a2].
) for many classes of hypergraphs, [a1], [a2].
The Vapnik–Chervonenkis dimension plays an important role in learning theory, especially in PAC learning (probably approximately correct learning). Thus, learnability of classes of 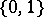 -valued functions is equivalent to finiteness of the Vapnik–Chervonenkis dimension, [a3].
-valued functions is equivalent to finiteness of the Vapnik–Chervonenkis dimension, [a3].
For the role of the Vapnik–Chervonenkis dimension in neural networks, see, e.g., [a4], [a5].
The independence number of a hypergraph 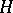 is the maximal cardinality of a subset
is the maximal cardinality of a subset 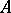 of
of 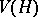 that does not contain any
that does not contain any 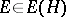 (see also Graph, numerical characteristics of a). This notion is closely related with
(see also Graph, numerical characteristics of a). This notion is closely related with 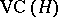 , [a6], [a7].
, [a6], [a7].
References
| [a1] | E. Kranakis, D. Krizanc, B. Ruf, J. Urrutia, G. Wöginger, "The VC-dimension of set systems defined by graphs" Discr. Appl. Math. , 77 : 3 (1997) pp. 237–257 |
| [a2] | C.H. Papadimitriou, M. Yannakakis, "On limited nondeterminism and the complexity of VC-dimension" J. Comput. Syst. Sci. , 53 : 2 (1996) pp. 161–170 |
| [a3] | S. Ben-David, N. Cesa-Bianchi, D. Haussler, P.M. Long, "Characterizations of learnability of 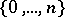 -valued functions" J. Comput. Syst. Sci. , 50 : 1 (1995) pp. 74–86 -valued functions" J. Comput. Syst. Sci. , 50 : 1 (1995) pp. 74–86 |
| [a4] | S.B. Holden, "Neural networks and the VC-dimension" J.G. McWhirter (ed.) , Mathematics in Signal Processing , III , Oxford Univ. Press (1994) pp. 73–84 |
| [a5] | W. Maass, "Perspectives of current research about the complexity of learning on neural nets" V. Roychowdhury (ed.) et al. (ed.) , Theoretical Advances in Neural Computation and Learning , Kluwer Acad. Publ. (1994) pp. 295–336 |
| [a6] | D.Q. Naiman, H.P. Wynn, "Independence number and the complexity of families of sets" Discr. Math. , 154 (1996) pp. 203–216 |
| [a7] | J. Pach, P.K. Agarwal, "Combinatorial geometry" , Wiley/Interscience (1995) pp. 247–254 |
Vapnik-Chervonenkis dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vapnik-Chervonenkis_dimension&oldid=39971