Valuation
logarithmic norm, norm on a field
A mapping 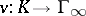 from a field
from a field 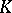 into
into 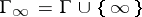 , where
, where 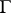 is a totally ordered Abelian group, the adjoined element
is a totally ordered Abelian group, the adjoined element 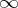 is assumed to be larger than any element of
is assumed to be larger than any element of 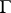 , and
, and 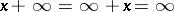 for all
for all 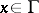 . Here the valuation must satisfy the following conditions:
. Here the valuation must satisfy the following conditions:
1) 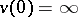 ,
, 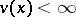 for
for  ;
;
2)  ;
;
3) 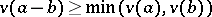 .
.
The image of 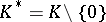 under
under  is a subgroup of
is a subgroup of 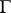 , called the value group of the valuation
, called the value group of the valuation  . Throughout what follows it is assumed that
. Throughout what follows it is assumed that 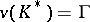 .
.
By the same axioms one defines logarithmic valuations of rings. Every ring with a non-Archimedean norm (cf. Norm on a field) can be made into a logarithmically-valued ring if one passes in the groupoid of values from the multiplicative to the additive notation and reverses the order. The element 0 is then naturally denoted by the symbol 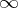 . The reverse transition from a ring with a logarithmic valuation to one with a non-Archimedean norm is also possible. If in a ring a non-Archimedean real norm is given, then the corresponding transition can be obtained by replacing each positive real number
. The reverse transition from a ring with a logarithmic valuation to one with a non-Archimedean norm is also possible. If in a ring a non-Archimedean real norm is given, then the corresponding transition can be obtained by replacing each positive real number 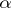 by
by 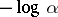 . The resulting logarithmic valuation is also called real.
. The resulting logarithmic valuation is also called real.
Two valuations 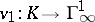 and
and 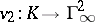 are said to be equivalent if there is an isomorphism
are said to be equivalent if there is an isomorphism 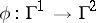 of ordered groups such that for all non-zero elements
of ordered groups such that for all non-zero elements 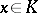 ,
,
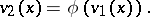 |
The set of those elements  of
of  for which
for which 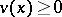 is a subring
is a subring 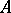 of
of 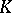 , called the valuation ring of
, called the valuation ring of  in
in 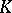 . It is always a local ring. The elements
. It is always a local ring. The elements  of
of 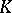 for which
for which 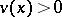 form a maximal ideal
form a maximal ideal 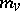 of
of 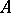 , called the valuation ideal of
, called the valuation ideal of  . The quotient ring
. The quotient ring 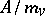 , which is a field, is called the residue field of the valuation
, which is a field, is called the residue field of the valuation  .
.
Let 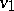 and
and 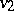 be two valuations on a field
be two valuations on a field 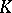 . The rings of these valuations, regarded as subrings of
. The rings of these valuations, regarded as subrings of 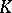 , are the same if and only if these valuations are equivalent. Thus, knowing all valuations of a field
, are the same if and only if these valuations are equivalent. Thus, knowing all valuations of a field 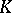 (up to equivalence) is the same as knowing all subrings that occur as valuation rings for this field. A subring
(up to equivalence) is the same as knowing all subrings that occur as valuation rings for this field. A subring 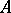 of
of 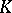 is a valuation ring for
is a valuation ring for 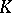 if and only if for every non-zero element
if and only if for every non-zero element 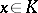 at least one of
at least one of  and
and 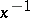 belongs to
belongs to 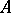 . Thus, a valuation ring can be defined abstractly as an integral ring (integral domain) that satisfies this condition relative to its field of fractions. Every such ring is the ring of the so-called canonical valuation for its field of fractions, for which the value group is
. Thus, a valuation ring can be defined abstractly as an integral ring (integral domain) that satisfies this condition relative to its field of fractions. Every such ring is the ring of the so-called canonical valuation for its field of fractions, for which the value group is 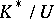 , where
, where  is the multiplicative group of invertible elements of
is the multiplicative group of invertible elements of 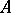 , and
, and 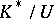 is ordered by divisibility.
is ordered by divisibility.
A valuation ring can be defined in yet another way. If  are two local rings with maximal ideals
are two local rings with maximal ideals 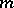 and
and  , respectively, then one says that
, respectively, then one says that 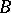 dominates
dominates 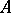 if
if 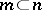 . Dominance is a partial order relation on the set of subrings of
. Dominance is a partial order relation on the set of subrings of 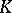 . The maximal elements of this set are exactly the valuation rings of
. The maximal elements of this set are exactly the valuation rings of 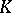 . If
. If 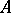 is a valuation ring and
is a valuation ring and 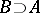 is a ring with the same field of fractions as
is a ring with the same field of fractions as 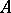 , then
, then 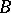 is also a valuation ring and is the localization of
is also a valuation ring and is the localization of 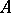 with respect to some prime ideal.
with respect to some prime ideal.
Examples of valuations.
1) The valuation defined by
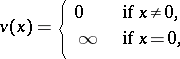 |
is called improper or trivial. Any valuation of a finite field is trivial.
2) Let 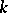 be a field and let
be a field and let 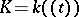 be the field of Laurent series over
be the field of Laurent series over 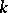 . Associating to a series
. Associating to a series 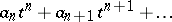 , where
, where 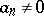 , its order
, its order  (and
(and 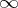 to the null series) is a valuation with value group
to the null series) is a valuation with value group 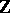 (the additive group of integers) and valuation ring
(the additive group of integers) and valuation ring 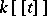 .
.
A valuation with values in 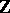 is called discrete; about their valuation rings see Discretely-normed ring. For a description of all valuations of the field of rational numbers, see [4].
is called discrete; about their valuation rings see Discretely-normed ring. For a description of all valuations of the field of rational numbers, see [4].
For each totally ordered Abelian group 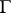 there is a valuation of a certain field with value group
there is a valuation of a certain field with value group 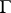 .
.
Ideals in valuation rings.
The set of ideals in a valuation ring is totally ordered by inclusion; every ideal of finite type is principal, that is, a valuation ring is a Bezout ring. A more complete description of the structure of ideals in a valuation ring can be given in terms of the value group of the valuation.
A subset 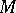 of a totally ordered set is said to be major if
of a totally ordered set is said to be major if 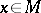 and
and 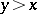 imply
imply 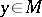 . Let
. Let 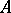 be the ring of a valuation
be the ring of a valuation  of a field
of a field  with value group
with value group 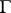 , let
, let 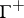 be the sub-semi-group of positive elements of
be the sub-semi-group of positive elements of 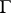 , and let
, and let 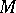 be a major set in
be a major set in 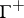 . The mapping
. The mapping 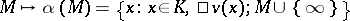 is a bijection between the set of major subsets of
is a bijection between the set of major subsets of 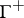 and the set of ideals of
and the set of ideals of 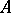 . Principal ideals correspond to majors having a minimal element. Prime ideals also correspond to majors of special form, namely:
. Principal ideals correspond to majors having a minimal element. Prime ideals also correspond to majors of special form, namely: 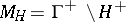 , where
, where 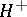 is the positive part of a convex subgroup
is the positive part of a convex subgroup  of
of 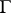 . Thus, there is a one-to-one correspondence between the prime ideals of
. Thus, there is a one-to-one correspondence between the prime ideals of 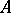 and the convex subgroups of the value group
and the convex subgroups of the value group 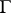 .
.
Let 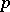 be the prime ideal corresponding to a convex subgroup
be the prime ideal corresponding to a convex subgroup 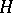 . Then the composite mapping
. Then the composite mapping 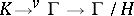 is a valuation of
is a valuation of 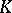 with valuation ring
with valuation ring 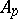 and valuation ideal
and valuation ideal 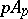 ; moreover, on the field
; moreover, on the field 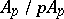 there is an induced valuation with values in
there is an induced valuation with values in 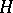 and valuation ring
and valuation ring  . In this manner a valuation splits into simpler ones. Let
. In this manner a valuation splits into simpler ones. Let 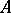 be a valuation ring. Then the prime spectrum of
be a valuation ring. Then the prime spectrum of 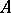 without the zero (
without the zero ( ) is a totally ordered set, and its type is called the height or rank of the corresponding valuation. If
) is a totally ordered set, and its type is called the height or rank of the corresponding valuation. If 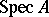 is finite, then the height of the valuation is the number of elements in
is finite, then the height of the valuation is the number of elements in 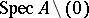 , and this is the same as the number of proper convex subgroups of
, and this is the same as the number of proper convex subgroups of 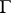 . A valuation of finite rank can be reduced to valuations of rank 1. The latter are characterized by the fact that their value groups are Archimedean (cf. Archimedean group), that is, they are isomorphic to a subgroup of the additive group
. A valuation of finite rank can be reduced to valuations of rank 1. The latter are characterized by the fact that their value groups are Archimedean (cf. Archimedean group), that is, they are isomorphic to a subgroup of the additive group 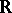 of real numbers. In this case the mapping
of real numbers. In this case the mapping 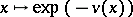 is an ultrametric norm on
is an ultrametric norm on 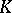 .
.
An important property of valuation rings is that they are integrally closed. Moreover, for an arbitrary integral ring 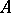 its integral closure is equal to the intersection of all valuation rings containing
its integral closure is equal to the intersection of all valuation rings containing 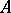 . A valuation ring is totally integrally closed if and only if its valuation is real, that is, has rank 1. A valuation ring is Noetherian if and only if the valuation is discrete.
. A valuation ring is totally integrally closed if and only if its valuation is real, that is, has rank 1. A valuation ring is Noetherian if and only if the valuation is discrete.
Valuations and topologies.
Let 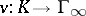 be a valuation on a field
be a valuation on a field  and let
and let 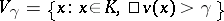 , where
, where 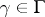 . The collection of all
. The collection of all 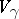 ,
, 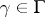 , is a fundamental system of neighbourhoods of zero for a topology
, is a fundamental system of neighbourhoods of zero for a topology 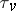 of
of 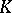 , which is said to be the topology determined by the valuation
, which is said to be the topology determined by the valuation  . It is separable and disconnected. The topology induced by
. It is separable and disconnected. The topology induced by 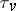 on
on 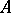 is, as a rule, different from that of a local ring. For a non-trivial valuation of
is, as a rule, different from that of a local ring. For a non-trivial valuation of 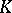 the topology
the topology 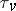 is locally compact if and only if
is locally compact if and only if  is discrete, the valuation ring is complete, and the residue field of
is discrete, the valuation ring is complete, and the residue field of  is finite;
is finite; 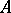 is then compact. The completion
is then compact. The completion 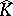 of
of 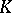 relative to
relative to 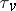 is a field;
is a field;  can be extended by continuity to a valuation
can be extended by continuity to a valuation 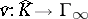 , and the topology of
, and the topology of 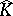 is the same as
is the same as 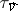 . The valuation ring
. The valuation ring 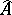 of
of 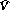 is the completion of the valuation ring
is the completion of the valuation ring 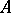 of
of  .
.
Two valuations 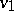 and
and  of
of 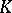 are called independent if the topologies
are called independent if the topologies  and
and 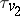 are distinct; this is equivalent to the fact that the valuation rings
are distinct; this is equivalent to the fact that the valuation rings 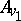 and
and 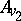 generate
generate 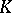 . Inequivalent valuations of height 1 are always independent. There is an approximation theorem for valuations: Let
. Inequivalent valuations of height 1 are always independent. There is an approximation theorem for valuations: Let 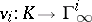 ,
, 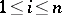 , be independent valuations, let
, be independent valuations, let 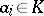 ,
, 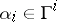 . Then there is an element
. Then there is an element  in
in 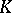 such that
such that 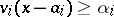 for all
for all 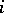 .
.
Extension of valuations.
If 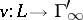 is a valuation of
is a valuation of 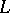 and
and 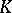 is a subfield of
is a subfield of 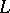 , then the restriction
, then the restriction 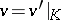 of
of 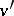 to
to 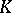 is a valuation of
is a valuation of 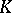 , and its value group
, and its value group 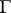 is a subgroup of
is a subgroup of 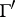 ;
; 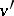 is then called an extension of
is then called an extension of  . Conversely, if
. Conversely, if  is a valuation on
is a valuation on 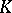 and
and  is an extension of
is an extension of 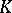 , then there is always a valuation of
, then there is always a valuation of  that extends
that extends  . The index
. The index 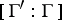 of
of 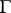 in
in 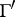 is called the ramification index of
is called the ramification index of 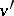 with respect to
with respect to  and is denoted by
and is denoted by  . The residue field
. The residue field 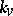 of
of  can be identified with a subfield of the residue field
can be identified with a subfield of the residue field 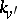 and the degree
and the degree 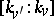 of the extension is denoted by
of the extension is denoted by 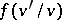 and is called the residue degree of
and is called the residue degree of 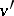 relative to
relative to  . An extension
. An extension 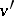 of a valuation
of a valuation  is said to be immediate if
is said to be immediate if  .
.
Let 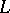 be an extension of
be an extension of 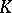 and let
and let 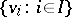 be the set of all extensions of
be the set of all extensions of  to
to 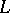 . If
. If 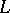 is a finite extension of
is a finite extension of 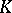 of degree
of degree  , then the set of all extensions of
, then the set of all extensions of  is finite, and
is finite, and
 |
In several cases equality holds, for example when  is discrete and either
is discrete and either 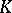 is complete or
is complete or 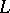 is separable over
is separable over 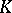 . If
. If 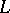 is a normal extension of
is a normal extension of 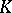 , then the extensions of
, then the extensions of  to
to 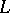 are permuted transitively by the
are permuted transitively by the 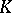 -automorphisms of
-automorphisms of 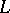 ; in particular, if
; in particular, if 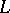 is a purely inseparable extension of
is a purely inseparable extension of 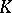 , then
, then  has only one extension. In the case of an arbitrary extension
has only one extension. In the case of an arbitrary extension 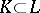 and an extension
and an extension 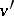 of a valuation
of a valuation  , the transcendence degree of
, the transcendence degree of 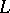 over
over 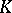 is greater than or equal to the sum
is greater than or equal to the sum
 |
where 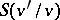 is the transcendence degree of the extension of the residue field of
is the transcendence degree of the extension of the residue field of 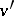 over that of
over that of  and
and 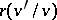 is the dimension of the space
is the dimension of the space 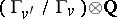 .
.
The concept of a valuation was introduced and studied by W. Krull in [1]. It is also widely used in algebraic geometry. Thus, in terms of "valuation rings" one can construct the abstract Riemann surface of a field (cf. [3]).
References
| [1] | W. Krull, "Allgemeine Bewertungstheorie" J. Reine Angew. Math. , 167 (1932) pp. 160–196 |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [3] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , Springer (1975) |
| [4] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
Comments
References
| [a1] | O. Endler, "Valuation theory" , Springer (1972) |
Valuation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Valuation&oldid=13681