Utility theory
A theory dealing with individual preferences and the representation of these by numerical functions. A preference relation on a set of alternatives  is a complete transitive binary relation
is a complete transitive binary relation 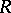 on
on 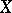 ; it is represented by a function
; it is represented by a function  on
on 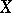 , and
, and 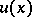 is called a utility function if for any
is called a utility function if for any 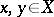 it follows from
it follows from 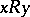 that
that 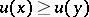 , and vice versa. Therefore utility theory deals with ordered sets and their monotone mappings into a numerical space (usually one-dimensional). Utility theory arose from researches by economists in the 18th century; the basis of modern utility theory was laid in the 1940s by J. von Neumann and O. Morgenstern [1].
, and vice versa. Therefore utility theory deals with ordered sets and their monotone mappings into a numerical space (usually one-dimensional). Utility theory arose from researches by economists in the 18th century; the basis of modern utility theory was laid in the 1940s by J. von Neumann and O. Morgenstern [1].
It is obvious that a utility function exists in the case of a finite set  . In the infinite case, a necessary and sufficient condition for the existence of a utility function is the existence of a utility-dense countable subset
. In the infinite case, a necessary and sufficient condition for the existence of a utility function is the existence of a utility-dense countable subset 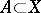 , i.e. for any
, i.e. for any 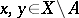 such that
such that 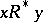 , there exists a
, there exists a 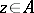 such that
such that 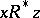 and
and 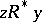 , where
, where 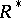 is a strong preference relation (
is a strong preference relation (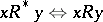 and not
and not 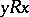 ). If
). If 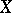 is a convex set in a vector space,
is a convex set in a vector space,  is continuous on
is continuous on 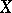 and for any
and for any 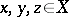 ,
, 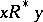 , and any
, and any 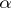 ,
,  , it is true that
, it is true that  , then there exists a linear utility function that is unique, up to a positive linear transformation [3]. Various combinations of weaker conditions lead to non-linear, discontinuous, or in some sense non-unique, utility functions. For example, if
, then there exists a linear utility function that is unique, up to a positive linear transformation [3]. Various combinations of weaker conditions lead to non-linear, discontinuous, or in some sense non-unique, utility functions. For example, if 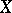 is a vector space, if it follows from
is a vector space, if it follows from 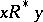 that
that 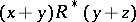 and if
and if 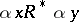 for all
for all 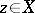 and
and 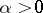 , the function is single-valued and piecewise linear.
, the function is single-valued and piecewise linear.
Utility theory also deals with stochastic ordering and ordering of the sums or differences of alternatives (in that case the utility function is constructed from a certain quaternary relation on  ), as well as with generalizations to
), as well as with generalizations to  -ary relations instead of binary ones, with the construction of a utility function at the same time with subjective probabilities, with the relation between the utility of multi-component alternatives and the utilities of the components, etc., [3], [4].
-ary relations instead of binary ones, with the construction of a utility function at the same time with subjective probabilities, with the relation between the utility of multi-component alternatives and the utilities of the components, etc., [3], [4].
References
| [1] | J. von Neumann, O. Morgenstern, "Theory of games and economic behavior" , Princeton Univ. Press (1947) |
| [2] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [3] | P.S. Fishburn, "Utility theory for decision making" , Wiley (1970) |
| [4] | P. Suppes, J. Zines, "Psychological measurements" , Moscow (1967) (In Russian; translated from English) |
Comments
Among other aspects of utility theory, one might mention transferable utility [a4], incomplete preferences [a1], non-standard utilities [a7], as well as the large body of literature concerning the (non-) significance of utility representations for economic theory (see, e.g., [a5] and [a6], but in the special case of concavifiable preference orderings one gets some measure of cardinal utility functions [a2], [a3]).
References
| [a1] | R.J. Aumann, , Human Judgement and Optimality , Wiley (1964) pp. 217–242 |
| [a2] | Y. Kannai, "The ALEP definition of complementary and least concave utility functions" J. Economic Th. , 22 (1980) pp. 115–117 |
| [a3] | Y. Kannai, , Generalized Concavity in Optimization and Economics , Acad. Press (1981) pp. 543–611 |
| [a4] | R.D. Luce, H. Raiffa, "Games and decisions. Introduction and critical survey" , Wiley (1957) |
| [a5] | P.A. Samuelson, "Foundations of economic analysis" , Harvard Univ. Press (1947) |
| [a6] | P.A. Samuelson, J. Economic Literature , 12 (1974) pp. 1255–1289 |
| [a7] | H. Skala, "Nonstandard utilities and the foundations of game theory" Internat. J. Game Theory , 3 (1974) pp. 67–81 |
| [a8] | R.M. Thrall (ed.) C.H. Coombs (ed.) R.L. Davis (ed.) , Decision processes , Wiley (1954) |
| [a9] | K.J. Arrow, F.H. Hahn, "General competitive analysis" , Oliver & Boyd (1971) |
| [a10] | G. Debreu, "Continuity properties of Paretian utility" Int. Econ. Review , 5 (1964) pp. 285–293 |
| [a11] | J.T. Rader, "The existence of a utility function to represent preferences" Rev. of Econ. Studies , XXX (1963) pp. 229–232 |
Utility theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Utility_theory&oldid=17247