Difference between revisions of "User:Whayes43"
| Line 31: | Line 31: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188019.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188019.png" /></td> </tr></table> | ||
| − | The independence is proved by exhibiting a model on which all the axioms are true except one. | + | The independence is proved by exhibiting a model on which all the axioms are true except one. |
| − | such a model is the series of natural numbers beginning with 1 | + | * For Axiom 1, such a model is the series of natural numbers beginning with $1$ |
| − | + | * For Axiom 2, it is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188020.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188022.png" /> | |
| − | it is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188020.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188022.png" /> | + | * For Axiom 3, it is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188023.png" /> |
| − | + | * For Axiom 4, it is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188024.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188025.png" /> | |
| − | the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188023.png" /> | + | * For Axiom 5, it is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188026.png" /> |
| − | |||
| − | the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188024.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188025.png" /> | ||
| − | |||
| − | the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188026.png" /> | ||
Sometimes one understands by Peano arithmetic the system in the first-order language with the function symbols <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188027.png" />, consisting of the axioms | Sometimes one understands by Peano arithmetic the system in the first-order language with the function symbols <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188027.png" />, consisting of the axioms | ||
Revision as of 17:09, 11 June 2015
A system of five axioms for the set of natural numbers  and a function
and a function  (successor) on it, introduced by G. Peano (1889):
(successor) on it, introduced by G. Peano (1889):
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  for any property
for any property  (axiom of induction).
(axiom of induction).
In the first version, Peano used $1$ instead of $0$ in Axioms 1, 3, and 5. Similar axioms were proposed by R. Dedekind (1888).
Peano's axioms are categorical, that is, any two systems  and
and  satisfying them are isomorphic. The isomorphism is determined by a function
satisfying them are isomorphic. The isomorphism is determined by a function  , where
, where
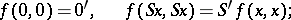 |
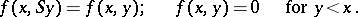 |
The existence of  for all pairs
for all pairs  and the mutual single-valuedness for
and the mutual single-valuedness for  are proved by induction. Peano's axioms make it possible to develop number theory; in particular, to introduce the usual arithmetic functions and to establish their properties. All the axioms are independent, but
are proved by induction. Peano's axioms make it possible to develop number theory; in particular, to introduce the usual arithmetic functions and to establish their properties. All the axioms are independent, but
and
can be combined to a single one:
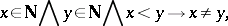 |
if one defines 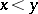 as
as
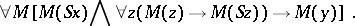 |
The independence is proved by exhibiting a model on which all the axioms are true except one.
- For Axiom 1, such a model is the series of natural numbers beginning with $1$
- For Axiom 2, it is the set
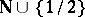 , where
, where  ,
, 
- For Axiom 3, it is the set

- For Axiom 4, it is the set
 with
with 
- For Axiom 5, it is the set

Sometimes one understands by Peano arithmetic the system in the first-order language with the function symbols  , consisting of the axioms
, consisting of the axioms
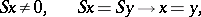 |
defining equalities for  and
and  , and the induction scheme
, and the induction scheme
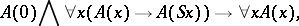 |
where  is an arbitrary formula, known as the induction formula (see Arithmetic, formal).
is an arbitrary formula, known as the induction formula (see Arithmetic, formal).
References
| [1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
Comments
The system of Peano arithmetic mentioned at the end of the article above is no longer categorical (cf. also Categoric system of axioms), and gives rise to so-called non-standard models of arithmetic.
References
| [a1] | H.C. Kennedy, "Peano. Life and works of Giuseppe Peano" , Reidel (1980) |
| [a2] | H.C. Kennedy, "Selected works of Giuseppe Peano" , Allen & Unwin (1973) |
| [a3] | E. Landau, "Grundlagen der Analysis" , Akad. Verlagsgesellschaft (1930) |
Whayes43. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whayes43&oldid=36465