Difference between revisions of "User:Whayes43"
| Line 1: | Line 1: | ||
| − | + | A system of five axioms for the set of natural numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718801.png" /> and a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718802.png" /> (successor) on it, introduced by G. Peano (1889): | |
| − | : | + | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718803.png" />; |
| − | : | + | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718804.png" />; |
| − | + | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718805.png" />; | |
| − | + | 4) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718806.png" />; | |
| − | :: | + | 5) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718807.png" /> for any property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718808.png" /> (axiom of induction). |
| − | The | + | In the first version 1 was used instead of 0. Similar axioms were proposed by R. Dedekind (1888). Peano's axioms are categorical, that is, any two systems <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p0718809.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188010.png" /> satisfying them are isomorphic. The isomorphism is determined by a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188011.png" />, where |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188012.png" /></td> </tr></table> | |
| − | == | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188013.png" /></td> </tr></table> |
| − | + | The existence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188014.png" /> for all pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188015.png" /> and the mutual single-valuedness for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188016.png" /> are proved by induction. Peano's axioms make it possible to develop number theory; in particular, to introduce the usual arithmetic functions and to establish their properties. All the axioms are independent, but | |
| − | + | and | |
| − | + | can be combined to a single one: | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188017.png" /></td> </tr></table> | |
| + | |||
| + | if one defines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188018.png" /> as | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188019.png" /></td> </tr></table> | ||
| + | |||
| + | The independence is proved by exhibiting a model on which all the axioms are true except one. For | ||
| + | |||
| + | such a model is the series of natural numbers beginning with 1; for | ||
| + | |||
| + | it is the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188020.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188022.png" />; for | ||
| + | |||
| + | the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188023.png" />; for | ||
| + | |||
| + | the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188024.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188025.png" />; for | ||
| + | |||
| + | the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188026.png" />. | ||
| + | |||
| + | Sometimes one understands by Peano arithmetic the system in the first-order language with the function symbols <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188027.png" />, consisting of the axioms | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188028.png" /></td> </tr></table> | ||
| + | |||
| + | defining equalities for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188030.png" />, and the induction scheme | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188031.png" /></td> </tr></table> | ||
| + | |||
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071880/p07188032.png" /> is an arbitrary formula, known as the induction formula (see [[Arithmetic, formal|Arithmetic, formal]]). | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951)</TD></TR></table> | ||
| + | |||
| + | |||
| + | |||
| + | ====Comments==== | ||
| + | The system of Peano arithmetic mentioned at the end of the article above is no longer categorical (cf. also [[Categoric system of axioms|Categoric system of axioms]]), and gives rise to so-called non-standard models of arithmetic. | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.C. Kennedy, "Peano. Life and works of Giuseppe Peano" , Reidel (1980)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.C. Kennedy, "Selected works of Giuseppe Peano" , Allen & Unwin (1973)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Landau, "Grundlagen der Analysis" , Akad. Verlagsgesellschaft (1930)</TD></TR></table> | ||
Revision as of 16:57, 11 June 2015
A system of five axioms for the set of natural numbers  and a function
and a function  (successor) on it, introduced by G. Peano (1889):
(successor) on it, introduced by G. Peano (1889):
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  for any property
for any property  (axiom of induction).
(axiom of induction).
In the first version 1 was used instead of 0. Similar axioms were proposed by R. Dedekind (1888). Peano's axioms are categorical, that is, any two systems  and
and  satisfying them are isomorphic. The isomorphism is determined by a function
satisfying them are isomorphic. The isomorphism is determined by a function  , where
, where
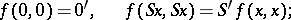 |
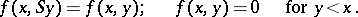 |
The existence of  for all pairs
for all pairs  and the mutual single-valuedness for
and the mutual single-valuedness for  are proved by induction. Peano's axioms make it possible to develop number theory; in particular, to introduce the usual arithmetic functions and to establish their properties. All the axioms are independent, but
are proved by induction. Peano's axioms make it possible to develop number theory; in particular, to introduce the usual arithmetic functions and to establish their properties. All the axioms are independent, but
and
can be combined to a single one:
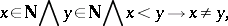 |
if one defines 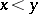 as
as
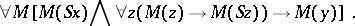 |
The independence is proved by exhibiting a model on which all the axioms are true except one. For
such a model is the series of natural numbers beginning with 1; for
it is the set 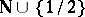 , where
, where  ,
,  ; for
; for
the set  ; for
; for
the set  with
with  ; for
; for
the set  .
.
Sometimes one understands by Peano arithmetic the system in the first-order language with the function symbols  , consisting of the axioms
, consisting of the axioms
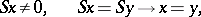 |
defining equalities for  and
and  , and the induction scheme
, and the induction scheme
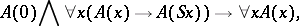 |
where  is an arbitrary formula, known as the induction formula (see Arithmetic, formal).
is an arbitrary formula, known as the induction formula (see Arithmetic, formal).
References
| [1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
Comments
The system of Peano arithmetic mentioned at the end of the article above is no longer categorical (cf. also Categoric system of axioms), and gives rise to so-called non-standard models of arithmetic.
References
| [a1] | H.C. Kennedy, "Peano. Life and works of Giuseppe Peano" , Reidel (1980) |
| [a2] | H.C. Kennedy, "Selected works of Giuseppe Peano" , Allen & Unwin (1973) |
| [a3] | E. Landau, "Grundlagen der Analysis" , Akad. Verlagsgesellschaft (1930) |
Whayes43. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whayes43&oldid=36440