Difference between revisions of "User:Richard Pinch/sandbox-6"
(TeX partly done) |
(TeX partly done) |
||
| Line 8: | Line 8: | ||
for all $a, b_i \in Q$ (cf. also [[Lattice]]; [[Distributivity]]; [[Associativity]]). | for all $a, b_i \in Q$ (cf. also [[Lattice]]; [[Distributivity]]; [[Associativity]]). | ||
| − | The name "quantale" was introduced by C.J. Mulvey [[#References|[a1]]] to provide a non-commutative extension of the concept of [[locale]]. The intention was to develop the concept of non-commutative topology introduced by R. Giles and H. Kummer [[#References|[a2]]], while providing a constructive, and non-commutative, context for the foundations of quantum mechanics and, more generally, non-commutative logic. The observation that the closed right ideals of a [[C*-algebra|$C*$-algebra]] form a quantale satisfying the conditions that each element is right-sided ($a \otimes 1_Q \le a$) and idempotent ($a \otimes a = a$)) led certain authors to restrict the term "quantale" to mean only quantales of this kind [[#References|[a3]]], but the term is now applied only in its original sense. | + | The name "quantale" was introduced by C.J. Mulvey [[#References|[a1]]] to provide a non-commutative extension of the concept of [[locale]]. The intention was to develop the concept of non-commutative topology introduced by R. Giles and H. Kummer [[#References|[a2]]], while providing a constructive, and non-commutative, context for the foundations of quantum mechanics and, more generally, non-commutative logic. The observation that the closed right ideals of a [[C*-algebra|$C^*$-algebra]] form a quantale satisfying the conditions that each element is right-sided ($a \otimes 1_Q \le a$) and idempotent ($a \otimes a = a$)) led certain authors to restrict the term "quantale" to mean only quantales of this kind [[#References|[a3]]], but the term is now applied only in its original sense. |
| − | The realization by J. Rosický [[#References|[a4]]] that the development of topological concepts such as regularity required additional structure led [[#References|[a5]]] to the consideration of involutive quantales, and of the spectrum $\text{Max} A$ of a $C*$-algebra $A$ (cf. also [[Spectrum of a C*-algebra|Spectrum of a $C*$-algebra]]) as the quantale of closed linear subspaces of $A$, together with the operations of join given by closed linear sum, product given by closed linear product of subspaces, and involution by involution within the $C*$-algebra. The right-sided elements of the spectrum $\text{Max} A$ are the closed right ideals of the $C*$-algebra $A$ (cf. [[#References|[a2]]], [[#References|[a6]]]). By the existence of approximate units, each element $a \in R(\text{Max} A)$ of the sup-lattice of right-sided elements satisfies the condition that $a \otimes a* \otimes a = a$. By a Gel'fand quantale $Q$ is meant an involutive unital quantale in which the right-sided (equivalently, left-sided) elements satisfy this condition. | + | The realization by J. Rosický [[#References|[a4]]] that the development of topological concepts such as regularity required additional structure led [[#References|[a5]]] to the consideration of involutive quantales, and of the spectrum $\text{Max} A$ of a $C^*$-algebra $A$ (cf. also [[Spectrum of a C*-algebra|Spectrum of a $C^*$-algebra]]) as the quantale of closed linear subspaces of $A$, together with the operations of join given by closed linear sum, product given by closed linear product of subspaces, and involution by involution within the $C^*$-algebra. The right-sided elements of the spectrum $\text{Max} A$ are the closed right ideals of the $C^*$-algebra $A$ (cf. [[#References|[a2]]], [[#References|[a6]]]). By the existence of approximate units, each element $a \in R(\text{Max} A)$ of the sup-lattice of right-sided elements satisfies the condition that $a \otimes a^* \otimes a = a$. By a Gel'fand quantale $Q$ is meant an involutive unital quantale in which the right-sided (equivalently, left-sided) elements satisfy this condition. |
Generalizing an observation in [[#References|[a4]]], the right-sided elements of any involutive quantale $Q$ may be shown to admit a pseudo-orthocomplement, defined by $a^\perp = \bigvee_{a* \otimes b = 0_Q} b$. In any Gel'fand quantale $Q$, the right-sided elements are idempotent, and the two-sided elements form a locale. | Generalizing an observation in [[#References|[a4]]], the right-sided elements of any involutive quantale $Q$ may be shown to admit a pseudo-orthocomplement, defined by $a^\perp = \bigvee_{a* \otimes b = 0_Q} b$. In any Gel'fand quantale $Q$, the right-sided elements are idempotent, and the two-sided elements form a locale. | ||
| − | Observing that relations on a set | + | Observing that relations on a set $X$ forming a quantale with respect to arbitrary union and composition is applied implicitly by C.A. Hoare and He Jifeng when considering the weakest pre-specification of a program [[#References|[a7]]], and noting that the quantale $Q(X)$ in question is exactly that of endomorphisms of the sup-lattice $\mathcal{P}(X)$ of subsets of $X \times X$, led to the consideration [[#References|[a8]]] of the quantale $Q(S)$ of endomorphisms of any orthocomplemented sup-lattice $S$, in which the involute $\alpha^*$ of a sup-preserving mapping $\alpha$ is defined by $s \alpha^* = \left({ \bigvee_{t \alpha \le s^\perp} t} \right)^\perp$ for each $s \in S$. In the quantale $Q(X)$ of relations on a set $X$, this describes the reverse of a relation in terms of complementation of subsets. Observing that the quantale $Q(H)$ of endomorphisms of the orthocomplemented sup-lattice of closed linear subspaces of a [[Hilbert space]] $H$ provides a motivating example for this quantization of the calculus of relations, the term Hilbert quantale was introduced for any quantale isomorphic to the quantale $Q9S)$ of an orthocomplemented sup-lattice $S$. |
Noting that the weak spectrum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001041.png" /> of a [[Von Neumann algebra|von Neumann algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001042.png" /> is a Gel'fand quantale of which the right-sided elements correspond to the projections of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001043.png" /> and on which the right pseudo-orthocomplement corresponds to orthocomplementation of projections, a Gel'fand quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001044.png" /> is said to be a von Neumann quantale if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001045.png" /> for any right-sided element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001046.png" />. For any von Neumann quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001047.png" />, the locale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001048.png" /> of two-sided elements is a complete [[Boolean algebra|Boolean algebra]]. Any Hilbert quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001049.png" /> is a von Neumann quantale, and a von Neumann quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001050.png" /> is a Hilbert quantale exactly if the canonical homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001051.png" />, assigning to each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001052.png" /> the sup-preserving mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001053.png" /> on the orthocomplemented sup-lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001054.png" /> of right-sided elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001055.png" />, is an isomorphism [[#References|[a8]]]. Any Hilbert quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001056.png" /> is a von Neumann factor quantale in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001057.png" /> is exactly <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001058.png" />. The weak spectrum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001059.png" /> of a von Neumann algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001060.png" /> is a factor exactly if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001061.png" /> is a factor [[#References|[a9]]] (cf. also [[Von Neumann algebra|von Neumann algebra]]). | Noting that the weak spectrum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001041.png" /> of a [[Von Neumann algebra|von Neumann algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001042.png" /> is a Gel'fand quantale of which the right-sided elements correspond to the projections of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001043.png" /> and on which the right pseudo-orthocomplement corresponds to orthocomplementation of projections, a Gel'fand quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001044.png" /> is said to be a von Neumann quantale if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001045.png" /> for any right-sided element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001046.png" />. For any von Neumann quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001047.png" />, the locale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001048.png" /> of two-sided elements is a complete [[Boolean algebra|Boolean algebra]]. Any Hilbert quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001049.png" /> is a von Neumann quantale, and a von Neumann quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001050.png" /> is a Hilbert quantale exactly if the canonical homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001051.png" />, assigning to each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001052.png" /> the sup-preserving mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001053.png" /> on the orthocomplemented sup-lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001054.png" /> of right-sided elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001055.png" />, is an isomorphism [[#References|[a8]]]. Any Hilbert quantale <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001056.png" /> is a von Neumann factor quantale in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001057.png" /> is exactly <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001058.png" />. The weak spectrum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001059.png" /> of a von Neumann algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001060.png" /> is a factor exactly if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q130/q130010/q13001061.png" /> is a factor [[#References|[a9]]] (cf. also [[Von Neumann algebra|von Neumann algebra]]). | ||
| Line 39: | Line 39: | ||
<TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Giles, H. Kummer, "A non-commutative generalization of topology" ''Indiana Univ. Math. J.'' , '''21''' (1971) pp. 91–102</TD></TR> | <TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Giles, H. Kummer, "A non-commutative generalization of topology" ''Indiana Univ. Math. J.'' , '''21''' (1971) pp. 91–102</TD></TR> | ||
<TR><TD valign="top">[a3]</TD> <TD valign="top"> K.I. Rosenthal, "Quantales and their applications" , ''Pitman Research Notes in Math.'' , '''234''' , Longman (1990)</TD></TR> | <TR><TD valign="top">[a3]</TD> <TD valign="top"> K.I. Rosenthal, "Quantales and their applications" , ''Pitman Research Notes in Math.'' , '''234''' , Longman (1990)</TD></TR> | ||
| − | <TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Rosický, "Multiplicative lattices and $C*$-algebras" ''Cah. Topol. Géom. Diff. Cat.'' , '''30''' (1989) pp. 95–110</TD></TR> | + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Rosický, "Multiplicative lattices and $C^*$-algebras" ''Cah. Topol. Géom. Diff. Cat.'' , '''30''' (1989) pp. 95–110</TD></TR> |
<TR><TD valign="top">[a5]</TD> <TD valign="top"> C.J. Mulvey, "Quantales" , ''Invited Lecture, Summer Conf. Locales and Topological Groups, Curaçao'' (1989)</TD></TR> | <TR><TD valign="top">[a5]</TD> <TD valign="top"> C.J. Mulvey, "Quantales" , ''Invited Lecture, Summer Conf. Locales and Topological Groups, Curaçao'' (1989)</TD></TR> | ||
| − | <TR><TD valign="top">[a6]</TD> <TD valign="top"> C.A. Akemann, "Left ideal structure of $C*$-algebras" ''J. Funct. Anal.'' , '''6''' (1970) pp. 305–317</TD></TR> | + | <TR><TD valign="top">[a6]</TD> <TD valign="top"> C.A. Akemann, "Left ideal structure of $C^*$-algebras" ''J. Funct. Anal.'' , '''6''' (1970) pp. 305–317</TD></TR> |
<TR><TD valign="top">[a7]</TD> <TD valign="top"> C.A.R. Hoare, He Jifeng, "The weakest prespecification" ''Inform. Proc. Lett.'' , '''24''' (1987) pp. 127–132</TD></TR> | <TR><TD valign="top">[a7]</TD> <TD valign="top"> C.A.R. Hoare, He Jifeng, "The weakest prespecification" ''Inform. Proc. Lett.'' , '''24''' (1987) pp. 127–132</TD></TR> | ||
<TR><TD valign="top">[a8]</TD> <TD valign="top"> C.J. Mulvey, J.W. Pelletier, "A quantisation of the calculus of relations" , ''Category Theory 1991, CMS Conf. Proc.'' , '''13''' , Amer. Math. Soc. (1992) pp. 345–360</TD></TR> | <TR><TD valign="top">[a8]</TD> <TD valign="top"> C.J. Mulvey, J.W. Pelletier, "A quantisation of the calculus of relations" , ''Category Theory 1991, CMS Conf. Proc.'' , '''13''' , Amer. Math. Soc. (1992) pp. 345–360</TD></TR> | ||
Revision as of 19:26, 12 August 2016
A complete sup-lattice $Q$ together with an associative product $\otimes$ satisfying the distributive laws $$ a \otimes \left({ \bigvee_i b_i }\right) = \bigvee_i a \otimes b_i $$ $$ \left({ \bigvee_i b_i }\right) \otimes a= \bigvee_i b_i \otimes a $$ for all $a, b_i \in Q$ (cf. also Lattice; Distributivity; Associativity).
The name "quantale" was introduced by C.J. Mulvey [a1] to provide a non-commutative extension of the concept of locale. The intention was to develop the concept of non-commutative topology introduced by R. Giles and H. Kummer [a2], while providing a constructive, and non-commutative, context for the foundations of quantum mechanics and, more generally, non-commutative logic. The observation that the closed right ideals of a $C^*$-algebra form a quantale satisfying the conditions that each element is right-sided ($a \otimes 1_Q \le a$) and idempotent ($a \otimes a = a$)) led certain authors to restrict the term "quantale" to mean only quantales of this kind [a3], but the term is now applied only in its original sense.
The realization by J. Rosický [a4] that the development of topological concepts such as regularity required additional structure led [a5] to the consideration of involutive quantales, and of the spectrum $\text{Max} A$ of a $C^*$-algebra $A$ (cf. also Spectrum of a $C^*$-algebra) as the quantale of closed linear subspaces of $A$, together with the operations of join given by closed linear sum, product given by closed linear product of subspaces, and involution by involution within the $C^*$-algebra. The right-sided elements of the spectrum $\text{Max} A$ are the closed right ideals of the $C^*$-algebra $A$ (cf. [a2], [a6]). By the existence of approximate units, each element $a \in R(\text{Max} A)$ of the sup-lattice of right-sided elements satisfies the condition that $a \otimes a^* \otimes a = a$. By a Gel'fand quantale $Q$ is meant an involutive unital quantale in which the right-sided (equivalently, left-sided) elements satisfy this condition.
Generalizing an observation in [a4], the right-sided elements of any involutive quantale $Q$ may be shown to admit a pseudo-orthocomplement, defined by $a^\perp = \bigvee_{a* \otimes b = 0_Q} b$. In any Gel'fand quantale $Q$, the right-sided elements are idempotent, and the two-sided elements form a locale.
Observing that relations on a set $X$ forming a quantale with respect to arbitrary union and composition is applied implicitly by C.A. Hoare and He Jifeng when considering the weakest pre-specification of a program [a7], and noting that the quantale $Q(X)$ in question is exactly that of endomorphisms of the sup-lattice $\mathcal{P}(X)$ of subsets of $X \times X$, led to the consideration [a8] of the quantale $Q(S)$ of endomorphisms of any orthocomplemented sup-lattice $S$, in which the involute $\alpha^*$ of a sup-preserving mapping $\alpha$ is defined by $s \alpha^* = \left({ \bigvee_{t \alpha \le s^\perp} t} \right)^\perp$ for each $s \in S$. In the quantale $Q(X)$ of relations on a set $X$, this describes the reverse of a relation in terms of complementation of subsets. Observing that the quantale $Q(H)$ of endomorphisms of the orthocomplemented sup-lattice of closed linear subspaces of a Hilbert space $H$ provides a motivating example for this quantization of the calculus of relations, the term Hilbert quantale was introduced for any quantale isomorphic to the quantale $Q9S)$ of an orthocomplemented sup-lattice $S$.
Noting that the weak spectrum 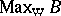 of a von Neumann algebra
of a von Neumann algebra 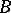 is a Gel'fand quantale of which the right-sided elements correspond to the projections of
is a Gel'fand quantale of which the right-sided elements correspond to the projections of 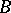 and on which the right pseudo-orthocomplement corresponds to orthocomplementation of projections, a Gel'fand quantale
and on which the right pseudo-orthocomplement corresponds to orthocomplementation of projections, a Gel'fand quantale 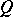 is said to be a von Neumann quantale if
is said to be a von Neumann quantale if 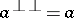 for any right-sided element
for any right-sided element 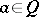 . For any von Neumann quantale
. For any von Neumann quantale 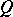 , the locale
, the locale 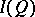 of two-sided elements is a complete Boolean algebra. Any Hilbert quantale
of two-sided elements is a complete Boolean algebra. Any Hilbert quantale 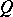 is a von Neumann quantale, and a von Neumann quantale
is a von Neumann quantale, and a von Neumann quantale 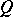 is a Hilbert quantale exactly if the canonical homomorphism
is a Hilbert quantale exactly if the canonical homomorphism 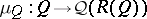 , assigning to each
, assigning to each 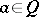 the sup-preserving mapping
the sup-preserving mapping 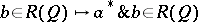 on the orthocomplemented sup-lattice
on the orthocomplemented sup-lattice 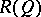 of right-sided elements of
of right-sided elements of 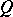 , is an isomorphism [a8]. Any Hilbert quantale
, is an isomorphism [a8]. Any Hilbert quantale 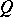 is a von Neumann factor quantale in the sense that
is a von Neumann factor quantale in the sense that 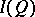 is exactly
is exactly 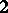 . The weak spectrum
. The weak spectrum 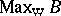 of a von Neumann algebra
of a von Neumann algebra 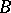 is a factor exactly if
is a factor exactly if 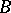 is a factor [a9] (cf. also von Neumann algebra).
is a factor [a9] (cf. also von Neumann algebra).
A homomorphism 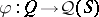 from a Gel'fand quantale
from a Gel'fand quantale 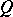 to the Hilbert quantale
to the Hilbert quantale 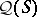 of an orthocomplemented sup-lattice
of an orthocomplemented sup-lattice 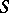 is said to be a representation of
is said to be a representation of 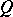 on
on 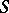 [a10]. A representation is said to be irreducible provided that
[a10]. A representation is said to be irreducible provided that 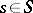 invariant (in the sense that
invariant (in the sense that 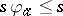 for all
for all 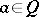 ) implies
) implies 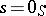 or
or 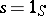 . The irreducibility of a representation
. The irreducibility of a representation 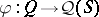 is equivalent to the homomorphism being strong, in the sense that
is equivalent to the homomorphism being strong, in the sense that 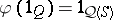 . A homomorphism
. A homomorphism 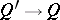 of Gel'fand quantales is strong exactly if
of Gel'fand quantales is strong exactly if 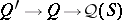 is irreducible whenever
is irreducible whenever 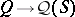 is irreducible. A representation
is irreducible. A representation 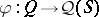 of
of 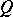 on an atomic orthocomplemented sup-lattice
on an atomic orthocomplemented sup-lattice 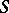 is said to be algebraically irreducible provided that for any atoms
is said to be algebraically irreducible provided that for any atoms 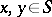 there exists an
there exists an 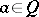 such that
such that 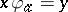 (cf. also Atomic lattice). Any algebraically irreducible representation is irreducible: the algebraically irreducible representations are those for which every atom is a cyclic generator. An algebraically irreducible representation
(cf. also Atomic lattice). Any algebraically irreducible representation is irreducible: the algebraically irreducible representations are those for which every atom is a cyclic generator. An algebraically irreducible representation 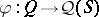 on an atomic orthocomplemented sup-lattice
on an atomic orthocomplemented sup-lattice 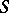 is said to be a point of the Gel'fand quantale
is said to be a point of the Gel'fand quantale 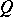 . The points of the spectrum
. The points of the spectrum 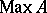 of a
of a 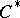 -algebra
-algebra 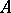 correspond bijectively to the equivalence classes of irreducible representations of
correspond bijectively to the equivalence classes of irreducible representations of 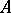 on a Hilbert space [a10]. (Presently (2000), this is subject to the conjecture that every point of
on a Hilbert space [a10]. (Presently (2000), this is subject to the conjecture that every point of 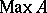 is non-trivial in the sense that there exists a pure state that maps properly. For a discussion of the role of pure states in this context, see [a10].) In particular, the spectrum
is non-trivial in the sense that there exists a pure state that maps properly. For a discussion of the role of pure states in this context, see [a10].) In particular, the spectrum 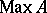 is an invariant of the
is an invariant of the 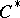 -algebra
-algebra 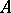 . It may be noted that the Hilbert quantale
. It may be noted that the Hilbert quantale 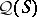 of an atomic orthocomplemented sup-lattice has, to within equivalence, a unique point; moreover, the reflection of such a Gel'fand quantale into the category of locales is exactly
of an atomic orthocomplemented sup-lattice has, to within equivalence, a unique point; moreover, the reflection of such a Gel'fand quantale into the category of locales is exactly 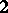 . In particular, the points of any locale are exactly its points in the sense of the theory of locales.
. In particular, the points of any locale are exactly its points in the sense of the theory of locales.
A von Neumann quantale 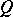 is said to be atomic provided that the orthocomplemented sup-lattice
is said to be atomic provided that the orthocomplemented sup-lattice 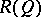 of its right-sided elements is atomic. For any atomic von Neumann quantale
of its right-sided elements is atomic. For any atomic von Neumann quantale 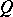 the complete Boolean algebra
the complete Boolean algebra 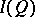 of two-sided elements is atomic. Moreover, the canonical homomorphism
of two-sided elements is atomic. Moreover, the canonical homomorphism 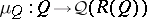 is algebraically irreducible exactly if
is algebraically irreducible exactly if 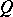 is a von Neumann factor quantale. A Gel'fand quantale
is a von Neumann factor quantale. A Gel'fand quantale 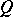 is said to be discrete provided that it is an atomic von Neumann quantale that admits a central decomposition of the unit
is said to be discrete provided that it is an atomic von Neumann quantale that admits a central decomposition of the unit 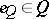 , in the sense that the atoms of the complete Boolean algebra
, in the sense that the atoms of the complete Boolean algebra 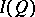 majorize a family of central projections with join
majorize a family of central projections with join 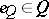 . For any atomic von Neumann algebra
. For any atomic von Neumann algebra 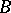 , the weak spectrum
, the weak spectrum 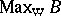 is a discrete von Neumann quantale. A locale
is a discrete von Neumann quantale. A locale 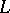 is a discrete von Neumann quantale exactly if it is a complete atomic Boolean algebra, hence the power set of its set of points. A homomorphism
is a discrete von Neumann quantale exactly if it is a complete atomic Boolean algebra, hence the power set of its set of points. A homomorphism 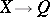 of Gel'fand quantales is said to be:
of Gel'fand quantales is said to be:
algebraically strong if 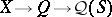 is algebraically irreducible whenever
is algebraically irreducible whenever 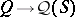 is an algebraically irreducible representation of
is an algebraically irreducible representation of 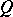 on an atomic orthocomplemented sup-lattice
on an atomic orthocomplemented sup-lattice 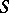 ;
;
a right embedding if it restricts to an embedding 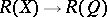 of the lattices of right-sided elements;
of the lattices of right-sided elements;
discrete if it is an algebraically strong right embedding. A Gel'fand quantale 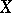 is said to be spatial if it admits a discrete homomorphism
is said to be spatial if it admits a discrete homomorphism 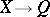 into a discrete von Neumann quantale
into a discrete von Neumann quantale 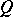 [a11]. For any
[a11]. For any 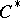 -algebra
-algebra 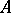 , the canonical homomorphism
, the canonical homomorphism
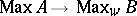 |
of its spectrum 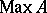 into the weak spectrum of its enveloping atomic von Neumann algebra
into the weak spectrum of its enveloping atomic von Neumann algebra 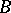 is discrete, hence
is discrete, hence 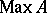 is spatial. Similarly, a locale
is spatial. Similarly, a locale 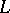 is spatial as a Gel'fand quantale exactly if its canonical homomorphism into the power set of its set of points is discrete. More generally, a Gel'fand quantale
is spatial as a Gel'fand quantale exactly if its canonical homomorphism into the power set of its set of points is discrete. More generally, a Gel'fand quantale 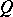 is spatial exactly if it has enough points, in the sense that if
is spatial exactly if it has enough points, in the sense that if 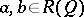 are distinct, then there is an algebraically irreducible representation
are distinct, then there is an algebraically irreducible representation  on an atomic orthocomplemented sup-lattice
on an atomic orthocomplemented sup-lattice 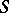 such that
such that 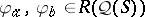 are distinct [a11].
are distinct [a11].
In other important directions, Girard quantales have been shown [a12] to provide a semantics for non-commutative linear logic, and Foulis quantales to generalize the Foulis semi-groups of complete orthomodular lattices [a13]. The concepts of quantal set and of sheaf have been introduced [a14] for the case of idempotent right-sided quantales, generalizing those for any locale. These concepts may be localized [a15] to allow the construction of a fibration from which the quantale may be recovered directly. The representation of quantales by quantales of relations has also been examined [a16].
References
| [a1] | C.J. Mulvey, "&" Rend. Circ. Mat. Palermo , 12 (1986) pp. 99–104 |
| [a2] | R. Giles, H. Kummer, "A non-commutative generalization of topology" Indiana Univ. Math. J. , 21 (1971) pp. 91–102 |
| [a3] | K.I. Rosenthal, "Quantales and their applications" , Pitman Research Notes in Math. , 234 , Longman (1990) |
| [a4] | J. Rosický, "Multiplicative lattices and $C^*$-algebras" Cah. Topol. Géom. Diff. Cat. , 30 (1989) pp. 95–110 |
| [a5] | C.J. Mulvey, "Quantales" , Invited Lecture, Summer Conf. Locales and Topological Groups, Curaçao (1989) |
| [a6] | C.A. Akemann, "Left ideal structure of $C^*$-algebras" J. Funct. Anal. , 6 (1970) pp. 305–317 |
| [a7] | C.A.R. Hoare, He Jifeng, "The weakest prespecification" Inform. Proc. Lett. , 24 (1987) pp. 127–132 |
| [a8] | C.J. Mulvey, J.W. Pelletier, "A quantisation of the calculus of relations" , Category Theory 1991, CMS Conf. Proc. , 13 , Amer. Math. Soc. (1992) pp. 345–360 |
| [a9] | J.W. Pelletier, "Von Neumann algebras and Hilbert quantales" Appl. Cat. Struct. , 5 (1997) pp. 249–264 |
| [a10] | C.J. Mulvey, J.W. Pelletier, "On the quantisation of points" J. Pure Appl. Algebra , 159 (2001) pp. 231–295 |
| [a11] | C.J. Mulvey, J.W. Pelletier, "On the quantisation of spaces" J. Pure Appl. Math. 175 (2002) pp.289-325 Zbl 1026.06018 |
| [a12] | D. Yetter, "Quantales and (non-commutative) linear logic" J. Symbolic Logic , 55 (1990) pp. 41–64 |
| [a13] | C.J. Mulvey, "Foulis quantales" to appear |
| [a14] | C.J. Mulvey, M. Nawaz, "Quantales: Quantal sets" , Non-Classical Logics and Their Application to Fuzzy Subsets: A Handbook of the Mathematical Foundations of Fuzzy Set Theory , Kluwer Acad. Publ. (1995) pp. 159–217 |
| [a15] | U. Berni-Canani, F. Borceux, R. Succi-Cruciani, "A theory of quantale sets" J. Pure Appl. Algebra , 62 (1989) pp. 123–136 |
| [a16] | C. Brown, D. Gurr, "A representation theorem for quantales" J. Pure Appl. Algebra , 85 (1993) pp. 27–42 |
Richard Pinch/sandbox-6. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Richard_Pinch/sandbox-6&oldid=39033