Difference between revisions of "User:Rafael.greenblatt/sandbox"
| Line 4: | Line 4: | ||
''Grassmann algebra, of a vector space $V$ over a field $k$'' | ''Grassmann algebra, of a vector space $V$ over a field $k$'' | ||
| − | An [[Associativity|associative algebra]] over $k$, the operation in which is denoted by the symbol $\wedge$, with generating elements $1,e_1,\ldots,e_n$ where $e_1,\ldots,e_n$ is a basis of$V$ , and with defining relations | + | An [[Associativity|associative algebra]] over $k$, the operation in which is denoted by the symbol $\wedge$, with generating elements $1,e_1,\ldots,e_n$ where $e_1,\ldots,e_n$ is a basis of $V$, and with defining relations |
$$ | $$ | ||
| Line 10: | Line 10: | ||
$$ | $$ | ||
| − | + | $$ | |
| + | 1 \wedge e_i = e_i \wedge 1 = e_i \qquad (i=1,\ldots,n), \qquad \ \wedge 1 = 1. | ||
| + | $$ | ||
| − | The exterior algebra does not depend on the choice of the basis and is denoted by | + | The exterior algebra does not depend on the choice of the basis and is denoted by $\wedge V$. The subspace $\wedge^r V$ ($r=0,1,\ldots$) in $\wedge V$ generated by the elements of the form $e_{i_1} \wedge \ldots \wedge e_{i_r}$ is said to be the $r$-th exterior power of the space $V$. The following equalities are valid: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708018.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708021.png" />. In addition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708022.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708024.png" />. The elements of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708025.png" /> are said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708027.png" />-vectors; they may also be regarded as skew-symmetric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708028.png" />-times contravariant tensors in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708029.png" /> (cf. [[Exterior product|Exterior product]]). |
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708030.png" />-vectors are closely connected with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708031.png" />-dimensional subspaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708032.png" />: Linearly independent systems of vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708033.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708034.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708035.png" /> generate the same subspace if and only if the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708036.png" />-vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708038.png" /> are proportional. This fact served as one of the starting points in the studies of H. Grassmann [[#References|[1]]], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708039.png" /> over a commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708040.png" /> with identity [[#References|[4]]]. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708041.png" />-th exterior power <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708043.png" />, of a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037 | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708030.png" />-vectors are closely connected with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708031.png" />-dimensional subspaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708032.png" />: Linearly independent systems of vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708033.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708034.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708035.png" /> generate the same subspace if and only if the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708036.png" />-vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708038.png" /> are proportional. This fact served as one of the starting points in the studies of H. Grassmann [[#References|[1]]], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708039.png" /> over a commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708040.png" /> with identity [[#References|[4]]]. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708041.png" />-th exterior power <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708043.png" />, of a module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037 | ||
Revision as of 13:48, 25 January 2012
(starting to modify "Exterior algebra")
Grassmann algebra, of a vector space $V$ over a field $k$
An associative algebra over $k$, the operation in which is denoted by the symbol $\wedge$, with generating elements $1,e_1,\ldots,e_n$ where $e_1,\ldots,e_n$ is a basis of $V$, and with defining relations
$$ e_i \wedge e_j = - e_j \wedge e_i \qquad (i,j=1,\ldots,n), \qquad e_i \wedge e_i = 0, $$
$$ 1 \wedge e_i = e_i \wedge 1 = e_i \qquad (i=1,\ldots,n), \qquad \ \wedge 1 = 1. $$
The exterior algebra does not depend on the choice of the basis and is denoted by $\wedge V$. The subspace $\wedge^r V$ ($r=0,1,\ldots$) in $\wedge V$ generated by the elements of the form $e_{i_1} \wedge \ldots \wedge e_{i_r}$ is said to be the $r$-th exterior power of the space $V$. The following equalities are valid:  ,
,  ,
,  ,
, 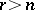 . In addition,
. In addition, 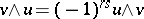 if
if  ,
, 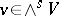 . The elements of the space
. The elements of the space 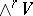 are said to be
are said to be  -vectors; they may also be regarded as skew-symmetric
-vectors; they may also be regarded as skew-symmetric  -times contravariant tensors in
-times contravariant tensors in  (cf. Exterior product).
(cf. Exterior product).
 -vectors are closely connected with
-vectors are closely connected with  -dimensional subspaces in
-dimensional subspaces in  : Linearly independent systems of vectors
: Linearly independent systems of vectors  and
and  of
of 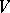 generate the same subspace if and only if the
generate the same subspace if and only if the  -vectors
-vectors 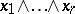 and
and 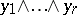 are proportional. This fact served as one of the starting points in the studies of H. Grassmann [1], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules
are proportional. This fact served as one of the starting points in the studies of H. Grassmann [1], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules  over a commutative ring
over a commutative ring 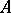 with identity [4]. The
with identity [4]. The  -th exterior power
-th exterior power  ,
, 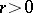 , of a module
, of a module is defined as the quotient module of the
 -th tensor power of this module by the submodule generated by the elements of the form
-th tensor power of this module by the submodule generated by the elements of the form  , where
, where  and
and  for certain
for certain 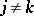 . The exterior algebra for
. The exterior algebra for 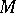 is defined as the direct sum
is defined as the direct sum  , where
, where 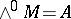 , with the naturally introduced multiplication. In the case of a finite-dimensional vector space this definition and the original definition are identical. The exterior algebra of a module is employed in the theory of modules over a principal ideal ring [5].
, with the naturally introduced multiplication. In the case of a finite-dimensional vector space this definition and the original definition are identical. The exterior algebra of a module is employed in the theory of modules over a principal ideal ring [5].
The Grassmann (or Plücker) coordinates of an  -dimensional subspace
-dimensional subspace  in an
in an  -dimensional space
-dimensional space 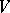 over
over  are defined as the coordinates of the
are defined as the coordinates of the  -vector in
-vector in 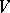 corresponding to
corresponding to  , which is defined up to proportionality. Grassmann coordinates may be used to naturally imbed the set of all
, which is defined up to proportionality. Grassmann coordinates may be used to naturally imbed the set of all  -dimensional subspaces in
-dimensional subspaces in 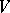 into the projective space of dimension
into the projective space of dimension 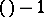 , where it forms an algebraic variety (called the Grassmann manifold). Thus one gets several important examples of projective algebraic varieties [6].
, where it forms an algebraic variety (called the Grassmann manifold). Thus one gets several important examples of projective algebraic varieties [6].
Exterior algebras are employed in the calculus of exterior differential forms (cf. Differential form) as one of the basic formalisms in differential geometry [7], [8]. Many important results in algebraic topology are formulated in terms of exterior algebras.
E.g., if 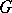 is a finite-dimensional
is a finite-dimensional 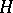 -space (e.g. a Lie group), the cohomology algebra
-space (e.g. a Lie group), the cohomology algebra 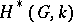 of
of 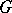 with coefficients in a field
with coefficients in a field 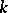 of characteristic zero is an exterior algebra with odd-degree generators. If
of characteristic zero is an exterior algebra with odd-degree generators. If 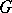 is a simply-connected compact Lie group, then the ring
is a simply-connected compact Lie group, then the ring 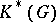 , studied in
, studied in 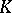 -theory, is also an exterior algebra (over the ring of integers).
-theory, is also an exterior algebra (over the ring of integers).
References
| [1] | H. Grassmann, "Gesammelte mathematische und physikalische Werke" , 1 , Teubner (1894–1896) pp. Chapt. 1; 2 |
| [2] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) |
| [3] | L.A. Kaluzhnin, "Introduction to general algebra" , Moscow (1973) (In Russian) |
| [4] | N. Bourbaki, "Elements of mathematics. Algebra: Multilinear algebra" , Addison-Wesley (1966) pp. Chapt. 2 (Translated from French) |
| [5] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [6] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1–3 , Cambridge Univ. Press (1947–1954) |
| [7] | S.P. Finikov, "Cartan's method of exterior forms in differential geometry" , 1–3 , Moscow-Leningrad (1948) (In Russian) |
| [8] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
Comments
Anticommuting variables (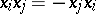 ,
, 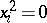 ) are sometimes called Grassmann variables; especially in the context of superalgebras, super-manifolds, etc. (cf. Super-manifold; Superalgebra). In addition the phrase fermionic variables occurs; especially in theoretical physics.
) are sometimes called Grassmann variables; especially in the context of superalgebras, super-manifolds, etc. (cf. Super-manifold; Superalgebra). In addition the phrase fermionic variables occurs; especially in theoretical physics.
References
| [a1] | C. Chevalley, "The construction and study of certain important algebras" , Math. Soc. Japan (1955) |
Rafael.greenblatt/sandbox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rafael.greenblatt/sandbox&oldid=20479