User:Maximilian Janisch/latexlist/Algebraic Groups/Deformation
A deformation of an analytic structure is a family of analytic spaces (or analytic objects connected with these spaces) depending on parameters (cf. Analytic space). The theory of deformations originated with the problem of classification of all possible pairwise non-isomorphic complex structures on a given differentiable real manifold. The fundamental idea (which must be credited to B. Riemann) was to introduce an analytic structure on the set of all such structures. The idea was made precise by the following concepts. An analytic family $x$ of complex manifolds parametrized by a complex space $5$ is defined as any smooth (i.e. locally structured as a projection of a direct product with smooth factors) analytic mapping $\pi : X \rightarrow S$. If $5$ is connected, then all fibres $X _ { S }$, $s \in S$, of $31$ are diffeomorphic to a fixed fibre $X$ where $o \in S$, and may be considered as a family of complex structures on $X$, analytically dependent on the parameter $s \in S$. If the fibres of the family $x$ consist all of complex manifolds diffeomorphic to $X$ and if all fibres are pairwise non-isomorphic, $5$ is said to be the moduli space of the real manifold $X$. A moduli space can also be defined for manifolds belonging to a specified class. The problem of constructing a moduli space (or the moduli problem) was first solved for compact Riemann surfaces (cf. Riemann surfaces, conformal classes of). Similar, though incomplete, results were also obtained for compact manifolds of complex dimension 2 (cf. Analytic surface).
Considerable difficulties are encountered in the study of moduli problems for higher-dimensional manifolds. In this context K. Kodaira and D.C. Spencer [6], [7], [8] made a local study of moduli problems, thus laying the foundations of the theory of deformation of complex manifolds and analytic bundles. An analytic deformation of a complex manifold $X$ is an analytic family $\pi : X \rightarrow S$, where $5$ is a complex space with a marked point $[ 7 ]$, with the fibre over it coinciding with $X$. The deformation $X = X _ { 0 } \times S$ is said to be trivial. A deformation $\pi : X \rightarrow S$ of the manifold $X$ is said to be isomorphic to the deformation $\pi : X \rightarrow S$ if there exists an analytic isomorphism $\phi : \tilde { X } \rightarrow X$ which is the identity on $X$ and which is such that $\pi \circ \phi = \tilde { \pi }$. If $\pi : X \rightarrow S$ is an analytic deformation, then any analytic mapping $f : S ^ { \prime } \rightarrow S$, where $S ^ { \prime }$ is a space with a marked point $0 ^ { \prime }$ and $f ( \mathfrak { o } ^ { \prime } ) = \mathfrak { o }$, defines by a base change a deformation $X \times S S ^ { \prime } \rightarrow S ^ { \prime }$; the inverse image of this deformation under the mapping $f$. The deformation $\pi : X \rightarrow S$ is said to be locally complete (at the point $[ 7 ]$) if any analytic deformation $\pi ^ { \prime } : X ^ { \prime } \rightarrow S ^ { \prime }$ of the manifold $X$ is isomorphic in some neighbourhood of the marked point to its inverse image for some local analytic mapping $f : S ^ { \prime } \rightarrow S$. If $d f _ { 0 } ^ { \prime }$ is unambiguously defined, the deformation is said to be versal at $[ 7 ]$, and if the germ of the mapping $f$ is uniquely defined, the deformation is said to be universal. An important role in the theory is played by the linear mapping $T _ { \emptyset } ( S ) \rightarrow H ^ { 1 } ( X _ { \diamond } , \Theta )$, where $\Theta = \Theta _ { X _ { 0 } }$ is the sheaf of germs of holomorphic vector fields on $X$, which is associated an analytic deformation and is named the corresponding infinitesimal deformation.
The principal theorem of the local theory of deformations, proved by M. Kuranishi [9], states that for each compact complex manifold $X$ there exists a deformation versal at the point $[ 7 ]$, which is parametrized by a (not necessarily smooth) analytic subspace $5$ in a neighbourhood of zero of the space $H ^ { 1 } ( X , \Theta )$. Here $5$ is the fibre at the point $[ 7 ]$ of some local analytic mapping $\gamma : H ^ { 1 } ( X _ { 0 } , \Theta ) \rightarrow H ^ { 2 } ( X _ { 0 } , \Theta )$ of the form $\gamma ( \xi ) = [ \xi , \xi ] + \ldots$, where $[ , ]$ is the operation in the graded Lie algebra $H ^ { * } ( X _ { \diamond } , \Theta )$ induced by the Lie bracket in the sheaf $( n$, the dots denoting terms of order 3 or higher. If $H ^ { 1 } ( X _ { 0 } , \Theta ) = 0$, the manifold $X$ is rigid, i.e. any deformation of it is locally trivial (the Fröhlicher–Nijenhuis rigidity theorem). If $H ^ { 2 } ( X , \Theta ) = 0$, $5$ is a neighbourhood of zero in $H ^ { 1 } ( X , \Theta )$. The tangent space $T _ { 0 } ( S )$ always coincides with $H ^ { 1 } ( X , \Theta )$. A deformation is complete at the point $[ 7 ]$ if and only if the corresponding infinitesimal deformation is surjective, and versality is equivalent to bijectivity of the infinitesimal deformation. If $H ^ { 0 } ( X _ { s } , \Theta _ { X _ { S } } )$, $s \in S$, is constant in a neighbourhood of $[ 7 ]$, the Kuranishi deformation is universal.
The local theory of deformations of compact complex manifolds may be generalized to include the case of compact complex spaces. The requirements that the mapping $\pi : X \rightarrow S$ be smooth and that the fibres be compact are then replaced by the requirements that $31$ be a proper flat mapping. Here, too, it is possible to prove the existence of a deformation versal at the point $[ 7 ]$ [3], [5], [11].
Studies are also conducted on the deformation of germs of analytic spaces (or, which amounts to the same thing, of analytic algebras). The theorem on the existence of a versal deformation for an isolated singular point of a complex space is valid [4].
In addition to the deformation theories of complex spaces, there also exist deformation theories of various "analytic objects" : analytic bundles, subspaces, mappings, cohomology classes, analytic spaces with additional structures (e.g. with polarization), etc. The principal deformations and the problems involved in these theories are similar to the ones described above. The results obtained for principal analytic bundles are also analogous to the ones above. In particular, for any principal analytic fibration (bundle) $k$ with compact base $x$ and complex Lie group $k$ as structure group there exists a deformation of $k$, versal at a point $[ 7 ]$, parametrized by an analytic subspace in a neighbourhood of zero of the space $H ^ { 1 } ( X , O _ { Ad } _ { E } )$ where $O _ { Ad } _ { E }$ is the sheaf of germs of holomorphic sections of the vector bundle over $x$ associated with $k$ by the adjoint representation [1]. If $x$ is a compact Riemann surface and $k$ is a reductive algebraic group, it is possible to construct moduli spaces for stable principal analytic bundles. In the theory of deformation of subspaces, on the contrary, one obtains quite general results of a global nature. Thus, if $x$ is an arbitrary complex space of finite dimension, a flat analytic family of compact analytic subspaces of $x$ (i.e. an analytic subspace $Y \subseteq X \times S$, where $5$ is a complex space and the projection $Y \rightarrow S$ is a proper flat mapping) has been constructed [2], and is a universal (in the global sense) deformation for any compact analytic subspace of $x$. In particular, $5$ is the moduli space for this problem. A similar moduli problem has also been solved in a related case, and also for compact analytic cycles of a given complex space. The solution of the moduli problem for compact subspaces also entails the solution of the moduli problem for analytic mappings of a given compact complex space into another given complex space.
Attempts have been made at a unification of the above deformation theories. Each one of these theories may be related to a contravariant functor $\Omega$ from the category of analytic spaces (or germs of analytic spaces) into the category of sets. For instance, in the theory of local deformations of a complex space $X$ the set $D ( S )$ consists of classes of locally isomorphic deformations of the space $X$ parametrized by an analytic space germ $5$. If $5$ and an element $\delta \in D ( S )$ are fixed, there results a morphism of functors $( . S ) \rightarrow D$. The surjectivity of this morphism (the pair $( S , \delta )$ is said to be complete in such a case) corresponds to the property of completeness of the deformation $0$, while the bijectivity corresponds to the property of its universality. In this way the moduli problem is connected with the problem of representability of the functor $\Omega$. This stimulated the study of covariant functors from the category of Artinian rings into the category of sets satisfying certain natural conditions [12]. The existence of a complete pair can be proved, but only in the category of formal algebras, which corresponds to the existence of a formally complete deformation (cf. Deformation of an algebraic variety below).
A generalization of the theory of deformations of complex structures on manifolds is the theory of deformations of a pseudo-group structure, the subject of which are families of pseudo-group structures smoothly depending on a parameter which assumes values in a real-analytic space. In particular, the existence of a versal deformation germ has been proved for a pseudo-group structure on a compact smooth manifold, corresponding to an elliptic transitive pseudo-group of transformations [10].
References
| [1] | I.F. Donin, "Construction of a versal family of deformations for holomorphic bundles over a compact complex space" Math. USSR Sb. , 23 : 3 (1974) pp. 405–416 Mat. Sb. , 94 : 3 (1974) pp. 430–443 MR393581 Zbl 0325.32008 |
| [2] | A. Douady, "Le problème des modules pour les sous-espaces analytiques compacts d'un espace analytique donné" Ann. Inst. Fourier , 16 (1966) pp. 1–95 MR0210935 MR0203082 |
| [3] | A. Douady, "Le problème des modules locaux pour les espaces $m$-analytiques compacts" Ann. Sci. Ecole Norm. Sup. , 7 : 4 (1974) pp. 569–602 MR382729 Zbl 0282.32014 |
| [4] | H. Grauert, "Ueber die Deformation isolierter Singularitäten analytischer Menge" Invent. Math. , 15 : 3 (1972) pp. 171–198 |
| [5] | H. Grauert, "Der Satz von Kuranishi für kompakte komplexe Räume" Invent. Math. , 25 : 2 (1974) pp. 107–142 MR0346194 Zbl 0286.32015 |
| [6] | K. Kodaira, D.C. Spencer, "On deformations of complex-analytic structures I" Ann. of Math. , 67 : 2 (1958) pp. 328–401 MR0112154 Zbl 0128.16901 |
| [7] | K. Kodaira, D.C. Spencer, "On deformations of complex-analytic structures II" Ann. of Math. , 67 : 3 (1958) pp. 403–466 MR112154 Zbl 0128.16901 |
| [8] | K. Kodaira, D.C. Spencer, "On deformations of complex-analytic structures III" Ann. of Math. , 71 : 1 (1960) pp. 43–76 MR0115189 Zbl 0128.16902 |
| [9] | M. Kuranishi, "New proof for the existence of locally complete families of complex structures" , Proc. Conf. Complex Analysis (Minneapolis, 1964) , Springer (1965) pp. 142–154 MR0176496 Zbl 0144.21102 |
| [10] | S.H. Moolgavkar, "On the existence of a universal germ of deformations for elliptic pseudogroup structures on compact manifolds" Trans. Amer. Math. Soc. , 212 : 485 (1975) pp. 173–197 MR0458515 Zbl 0308.58014 |
| [11] | V.P. Palamodov, "Deformations of complex spaces" Russian Math. Surveys , 31 : 3 (1976) pp. 129–197 Usphekhi Mat. Nauk , 31 (1976) pp. 129–194 MR0508121 MR0435451 Zbl 0355.32020 Zbl 0347.32009 |
| [12] | M. Schlessinger, "Functors of Artin rings" Trans. Amer. Math. Soc. , 130 (1968) pp. 208–222 MR0217093 Zbl 0167.49503 |
Comments
Instead of "infinitesimal deformation" it is usual to speak of "Kodaira–Spencer mappingKodaira–Spencer mapping" . For some results and concepts cf. [a1]–[a5]. A comprehensive treatment of the Kodaira–Spencer theory of deformation is [a6].
References
| [a1] | J. Gasqui, H. Goldschmidt, "Complexes of differential operators and symmetric spaces" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 797–828 MR0981631 Zbl 0666.58041 |
| [a2] | J. Gasqui, H. Goldschmidt, "Some rigidity results in the deformation theory of symmetric spaces" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 839–851 MR0981633 Zbl 0698.53034 |
| [a3] | J. Gasqui, H. Goldschmidt, "Deformations infinitesimals des structures conformes plates" , Birkhäuser (1984) |
| [a4] | R. Hermann, "Geometric and Lie-theoretic principles in pure and applied deformation theory" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 701–796 MR0981630 Zbl 0685.58038 |
| [a5] | J.F. Pommaret, "Deformation theory of geometric and algebraic structures" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 829–838 MR0981632 Zbl 0684.58047 |
| [a6] | K. Kodaira, "Complex manifolds and deformations of complex structures" , Springer (1986) MR0815922 |
A deformation of an algebraic variety is the inclusion of the algebraic variety into a family of algebraic varieties. The theory of deformation of algebraic varieties and schemes is the algebraic analogue of the theory of deformation of analytic structures. Its principal problems are listed below.
Existence of a lift. Let $X _ { 0 }$ be a scheme over a field $k$, let $5$ be a scheme and let $s _ { 0 } \in S$ be a point with the residue field $k ( s _ { 0 } ) = k$. Does a flat $5$-scheme $x$ for which the fibre $X _ { 0 }$ over the point $S D$ is isomorphic to $X _ { 0 }$ exist? (The $5$-scheme $x$ is known as the deformation or lift of the scheme $X _ { 0 }$ over $5$.)
The universality problem. Does a versal (respectively, universal) deformation of a scheme $X _ { 0 }$ (i.e. a deformation $N$ over the scheme $X _ { 0 }$ such that for any other deformation $X \rightarrow S$ it is possible to find a (respectively, a unique) morphism $S \rightarrow M$ for which $X \cong M \times M S$) exist?
Any deformation $X \rightarrow S$ of the scheme $X _ { 0 }$ by the operation of formal completion along the fibre $X _ { 0 }$ defines a formal deformation $K$ over the completion of the local ring $O _ { S , S _ { 0 } }$ of the scheme $5$ at the point $S D$, i.e. a dense formal scheme over $\hat { \mathscr { O } } _ { S , s _ { 0 } }$ with topological space $X _ { 0 }$. The formal analogues of the problems listed above are formulated as follows:
Existence of a formal deformation. Let a complete local ring $1$ with the residue field $k$ be given. Does a flat formal scheme over $1$ with topological space $X _ { 0 }$ exist?
Existence of a formal moduli scheme. Does a formal versal (respectively, universal) deformation, i.e. a flat formal scheme $p : \kappa \rightarrow O$ over a complete local ring $0$ with the residue field $k$ such that for any formal deformation $\kappa ^ { \prime } \rightarrow \operatorname { Spec } \Lambda$ there is a (respectively, a unique) ring homomorphism $O \rightarrow \Lambda$ for which $\kappa ^ { \prime } \cong \kappa \otimes O \Lambda$, exist?
A universal formal deformation of a smooth variety represents the algebraic analogue of a local moduli space in the theory of deformation of analytic structures.
If $S = \text { Spec } R$, where $R$ is a local Artinian (respectively, complete) ring with residue field $k$, the deformation of $X _ { 0 }$ over $5$ is said to be infinitesimal (respectively, effective formal). If $R$ is a complete local ring of characteristic zero (e.g. the ring of Witt vectors, cf. Witt vector), the effective formal deformation of $X _ { 0 }$ is said to be the lift of $X _ { 0 }$ into characteristic zero.
If $X _ { 0 }$ is a smooth $k$-scheme and $H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } ) = 0$, where $T _ { X _ { 0 } }$ is the tangent bundle on $X _ { 0 }$, then for any Artinian (respectively, complete) local ring there exists an infinitesimal (respectively, formal) deformation of $X _ { 0 }$. Moreover, if $H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } ) = 0$, such a deformation is unique up to isomorphism [4]. Similar statements for not necessarily smooth schemes are given in terms of the cotangent complex [5], [6]. The problem of the existence of an effective formal deformation is studied by means of the functor $D _ { X _ { 0 } }$ from the category $C _ { i }$ of local Artinian rings with residue field $k$ into the category of sets which associates to each object $R$ from $C _ { i }$ the set of all infinitesimal deformations of $X _ { 0 }$ over $R$. A universal formal deformation of $X _ { 0 }$ exists if and only if the functor is a pro-representable functor. Here, a pro-representing object — a complete local ring $M _ { X _ { 0 } }$ with residue field $k$ — is said to be a formal scheme of moduli of the $k$-scheme $X _ { 0 }$. A formal versal deformation $\tilde { \rho } : \tilde { \kappa } \rightarrow \tilde { M } _ { X _ { 0 } }$ exists if $X _ { 0 }$ is proper over $k$ or if $X _ { 0 }$ is an affine scheme of finite type over $k$ with isolated singular points [2], [6]. A versal formal deformation is universal if for any surjective homomorphisms $R ^ { \prime } \rightarrow R$ of Artinian local rings, and any deformation $X ^ { \prime } \rightarrow R ^ { \prime }$ from $D _ { X _ { 0 } } ( R ^ { \prime } )$ the natural mapping of automorphism groups
\begin{equation} \operatorname { Aut } _ { R ^ { \prime } } ( X ^ { \prime } | X _ { 0 } ) \rightarrow \operatorname { Aut } _ { R } ( X _ { R ^ { \prime } } ^ { \prime } \otimes R | X _ { 0 } ) \end{equation}
is surjective. This condition is satisfied, for example, if $X _ { 0 }$ is a smooth scheme and $H ^ { 0 } ( X _ { 0 } , T _ { X _ { 0 } } ) = 0$. Here, if $H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } ) = 0$, the formal scheme of moduli $M _ { X _ { 0 } }$ is a complete regular local ring which is isomorphic to the ring $k [ [ t _ { 1 } , \ldots , t _ { m } ] ]$ of formal power series in $m$ variables. In this case the number $m$ is equal to $H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } )$ and is called the number of local moduli of the scheme $X _ { 0 }$. In the general case $H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } )$ is equal to the dimension of the space tangent to $M _ { X _ { 0 } }$ and $\hat { M } _ { X _ { 0 } }$, i.e. to the dimension $12$, where $m$ is the maximal ideal of the corresponding local ring, and
\begin{equation} \operatorname { dim } _ { k } H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } ) - \operatorname { dim } M _ { X _ { 0 } } \leq \operatorname { dim } _ { k } H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } ) \end{equation}
The presence of nilpotent elements in a formal scheme of moduli is a fairly frequent phenomenon.
If the versal (respectively, universal) formal deformation $\kappa \rightarrow M X _ { 0 }$ is algebraizable, i.e. if there exists a flat scheme over $M _ { X _ { 0 } }$ the formal completion of which along a closed fibre is isomorphic to $K$, the corresponding algebraization is said to be a local versal (respectively, universal) deformation of the $k$-scheme $X _ { 0 }$. If $X _ { 0 }$ is projective and $H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } ) = 0$, the algebraization exists. Thus, for a smooth curve of genus $g > 1$ there exists a local universal deformation over the ring $k [ [ t ] , \dots , t ] g - 3 ]$. In the general case, for each polarization $6$ of the variety $X _ { 0 }$ there exists a maximal closed subscheme of moduli $M X _ { 0 } , \alpha \subset M X _ { 0 }$ such that $p ^ { - 1 } ( M x _ { 0 } , \alpha )$ is algebraizable. The codimension of 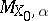 in $M _ { X _ { 0 } }$ does not exceed $\operatorname { dim } _ { k } H ^ { 2 } ( X _ { 0 } , O _ { X _ { 0 } } )$. Thus, if $X _ { 0 }$ is an algebraic $K 3$-surface, $M _ { X _ { 0 } }$ is regular of dimension 20, and for any polarization $6$ the subscheme
in $M _ { X _ { 0 } }$ does not exceed $\operatorname { dim } _ { k } H ^ { 2 } ( X _ { 0 } , O _ { X _ { 0 } } )$. Thus, if $X _ { 0 }$ is an algebraic $K 3$-surface, $M _ { X _ { 0 } }$ is regular of dimension 20, and for any polarization $6$ the subscheme 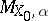 is regular of dimension 19.
is regular of dimension 19.
Artin's approximation theorem is used in the algebraization of formal schemes of moduli. There exists a scheme $5$ of finite type over $k$ and a point $s _ { 0 } \in S$ with residue field $k$ such that the completion $\mathscr { O } _ { S , s _ { 0 } } \simeq \hat { M } _ { X _ { 0 } }$, and there exists a deformation of $X _ { 0 }$ over $5$ inducing the versal local deformation $\tilde { p } : \tilde { \kappa } \rightarrow \hat { M } _ { X _ { 0 } }$. The scheme $5$ is defined uniquely up to a local isomorphism in the étale topology [1]. For the deformation of singular varieties and singular points see Singular point of an algebraic variety. For the deformation of group schemes see Group scheme.
References
| [1] | M. Artin, "Algebraic approximation of structures over complete local rings" Publ. Math. IHES , 36 (1969) pp. 23–58 MR0268188 Zbl 0181.48802 |
| [2] | I.V. Dolgachev, V.A. Iskovskikh, "Geometry of algebraic varieties" Russian Math. Surveys , 5 : 6 (1976) pp. 803–864 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 12 (1974) pp. 77–170 |
| [3] | M. Schlessinger, "Functors of Artin rings" Trans. Amer. Math. Soc. , 130 (1968) pp. 208–222 MR0217093 Zbl 0167.49503 |
| [4] | A. Grothendieck (ed.) et al. (ed.) , Révètement étales et groupe fondamental, SGA 1 , Lect. notes in math. , 224 , Springer (1971) MR2017446 |
| [5] | D.S. Rim, "Formal deformation theory" A. Grothendieck (ed.) et al. (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7 , Lect. notes in math. , 288 , Springer (1972) pp. 32–132 Zbl 0246.14001 |
| [6] | D. Mumford, O. Zariski (ed.) , Algebraic surfaces , Springer (1971) pp. 118–128 MR0469915 Zbl 0138.42002 |
I.V. Dolgachev
A deformation of algebras is a family of algebras depending or parameters. All possible bilinear operations or algebras $3$ in a space $V$ over a field $k$ form a vector space, $A ( N )$. Two elements of this space represent isomorphic algebras if and only if they lie on the same orbit of the linear group $GL ( V )$, acting naturally on $A ( N )$. The theory of deformation of algebras makes it possible to study the local structure of the quotient set $A ( V ) / GL ( V )$, i.e. the set of classes of isomorphic algebras in the space $V$, a direct description of which involves considerable difficulties. If a certain class of algebras $K \subseteq A ( V )$ is isolated, one may consider the deformation of the algebras in $K$ that stay within that class. In particular, one may consider deformations of associative and associative-commutative algebras and Lie algebras, which form the classes $K = Ass ( V )$, $K = \operatorname { Comm } ( V )$, $K = \operatorname { Lie } ( V )$, respectively, which are invariant with respect to the action of the group $GL ( V )$. If $\operatorname { dim } V = n$, these classes are algebraic varieties in the $12$-dimensional space $A ( N )$.
The theory of deformation of algebras in a finite-dimensional space $V$ over the field $k = R , C$ of real or complex numbers in many respects resembles the theory of deformations of analytic structures. Each finite-dimensional algebra $3$ over $k = R$ or $m$ has a complete deformation parametrized by an analytic subspace germ in the zero of the space $H ^ { 2 } ( \mathfrak { A } , V )$ (if $H ^ { 3 } ( \mathfrak { A } , V ) = 0$ this subspace coincides with $H ^ { 2 } ( \mathfrak { A } , V )$). The rigidity theorem immediately follows from this fundamental result: If $H ^ { 2 } ( \mathfrak { A } , V ) = 0$, the algebra $3$ is rigid in $K$, i.e. the orbit of an element of $3$ with respect to $GL ( V )$ is open in $K$. Thus, semi-simple Lie algebras, as well as their Borel subalgebras, are rigid in the class of Lie algebras. The converse proposition is not true. Analogous theorems are valid for finite-dimensional algebras over an arbitrary algebraically closed field $k$. For instance, if $H ^ { 2 } ( G , V ) = 0$, the orbit of the algebra $3$ in $\overline { k }$ is Zariski open.
The theory of deformation of homomorphisms of one finite-dimensional algebra into another may be developed in an analogous manner. In fact, the theories described above form part of a general scheme which involves the use of graded Lie algebras. Similar results have also been obtained for the deformation of subalgebras.
In addition to the above theory there also exists the theory of formal deformations of algebras and their homomorphisms over an arbitrary field $k$. A formal deformation of an algebra defined in a vector space $V$ over $k$ is an algebra over the space $V \otimes k ( ( t ) )$ over the field $k ( ( t ) )$ of formal power series over $k$ with the operation $6$ which is fully determined by the condition
\begin{equation} \alpha \circ b = \alpha b + \sum _ { i = 1 } ^ { \infty } \phi _ { i } ( \alpha , b ) t ^ { i } , \quad \alpha , b \in V \end{equation}
where $\phi _ { i } \in A ( V )$. In requiring the deformation to belong to a given class of algebras, one may speak of formal deformations of associative, associative-commutative, Lie, and other algebras.
Two formal deformations of an algebra $3$ with the multiplications $x$ and $6$, respectively, are said to be equivalent if there exists a linear automorphism $\Phi$ of the space $V \otimes k ( ( t ) )$ with the property
\begin{equation} \Phi ( \alpha ) = \alpha + \sum _ { i = 1 } ^ { \infty } t ^ { i } \phi _ { i } ( \alpha ) , \quad \alpha \in V \end{equation}
where $\phi _ { i } : V \rightarrow V$ is a linear mapping, such that
\begin{equation} a \circ b = \Phi ^ { - 1 } ( \Phi ( \alpha ) \times \Phi ( b ) ) \end{equation}
A deformation which is equivalent to the algebra $3$ with the initial multiplication is known as trivial. An algebra without non-trivial formal deformations in a given class of algebras is known as formally rigid in that class. For instance, the free algebra in the class of all algebras will be formally rigid. In the classes $( V )$, 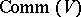 and $( V )$ the equation $H ^ { 2 } ( \mathfrak { A } , V ) = 0$ is a sufficient condition of formal rigidity of the algebra $3$; in the class $( V )$ it is also a necessary condition [3].
and $( V )$ the equation $H ^ { 2 } ( \mathfrak { A } , V ) = 0$ is a sufficient condition of formal rigidity of the algebra $3$; in the class $( V )$ it is also a necessary condition [3].
If $k = R$ or $m$, formal deformations of algebras are a tool in the study of analytic deformations.
An important field of applications and a source of examples of deformations of algebras is theoretical physics, in which, in particular, the following class of deformations of an algebra arose [4], [5]. A contraction of a finite-dimensional algebra $3$ over $k = R$ or $m$ is a continuous curve $\Omega _ { t }$, $0 \leq t \leq 1$. The algebra $21$ obtained from $3$ by a contraction is known as the limit algebra and need not be isomorphic to the algebra $3$. For instance, any algebra may be contracted into an algebra with zero multiplication; any semi-simple Lie algebra may be contracted into a non-Abelian non-semi-simple algebra.
References
| [1a] | A. Nijenhuis, R.W. Richardson Jr., "Cohomology and deformations in graded Lie algebras" Bull. Amer. Math. Soc. , 72 : 1 (1966) pp. 1–29 MR0195995 Zbl 0136.30502 |
| [1b] | A. Nijenhuis, R.W. Richardson Jr., "Deformations of homomorphisms of Lie groups and Lie algebras" Bull. Amer. Math. Soc. , 73 : 1 (1967) pp. 175–179 MR0204575 Zbl 0153.04402 |
| [2] | M. Gerstenhaber, "On the deformation of rings and algebras" Ann. of Math. , 79 (1964) pp. 59–103 MR0171807 Zbl 0123.03101 |
| [3] | D. Knudson, "On the deformation of commutative algebras" Trans. Amer. Math. Soc. , 140 (1969) pp. 55–70 MR0240091 Zbl 0199.36102 |
| [4] | E. Inönü, E.P. Wigner, "On the contraction of groups and their representations" Proc. Nat. Acad. Sci. USA , 39 : 6 (1953) pp. 510–524 MR0055352 Zbl 0050.02601 |
| [5] | R. Hermann, "Lie groups for physicists" , Benjamin (1966) MR0213463 Zbl 0135.06901 |
A.A. BoyarkinA.V. MikhalevA.L. Onishchik
Comments
In recent years ideas from non-standard analysis have been applied to deformation problems in algebra. In particular, by this approach rigidity results for Lie algebras have been obtained also in cases with non-vanishing cohomology. For the use of techniques from non-standard analysis in the theory of deformation of algebras, cf. [a9], [a10].
It has now become clear that the deformation theory of algebras is not merely analogous to that of analytic structures but that there are in fact fundamental relations between the two subjects. In particular, the formal deformation theory of a smooth compact complex algebraic variety $x$ can be reduced to that of a single ring built from $x$. There is also a relationship between the classical Hodge decomposition of the cohomology of an analytic manifold and the recent Hodge decomposition of the cohomology of a commutative algebra, [a1].
For the relation between deformations of singular and non-singular Riemann surfaces and the deformation theory of the corresponding algebra of analytic functions, cf. [a2].
In the theory of operator and Banach algebras one studies whether algebras close to the given one (in the metric sense) are isomorphic, cf. [a3]–[a5].
There is a deformation-theoretic approach to quantization based on the so-called star-products, which are non-commutative deformations of the commutative product of the ring of functions on a manifold, cf. [a6]–[a8].
For deformations of meromorphic differential equations cf. [a11].
Reference [a12] provides an up-to-date (1988) survey of many aspects of deformation theory, with the notable omission of deformations (bendings) of convex surfaces, resolution of singularities, deformations of vector fields and such in the setting of structural stability of dynamical systems, isospectral and isomonodromy deformations in the setting of integrable systems, and deformations of mechanical structures and solid bodies. Cf. also Deformation, isometric; Deformation over a principal base; Deformation tensor; Integrable system; Resolution of singularities; Stability of an elastic system; Stability in the presence of persistently-acting perturbations; and Perturbation theory, which contain information on other aspects of deformation theory than the ones dealt with above and in [a12].
References
| [a1] | M. Gerstenhaber, D. Shack, "Algebraic cohomology and deformation theory" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 11–264 MR0981619 Zbl 0676.16022 |
| [a2] | R. Rochberg, "Deformation theory for algebras of analytic functions" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 501–536 MR0981625 Zbl 0701.46042 |
| [a3] | E. Christensen, "Close operator algebras" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 537–556 MR0981626 Zbl 0672.46031 |
| [a4] | K. Jarosz, "Perturbations of Banach algebras" , Springer (1985) MR0788884 Zbl 0557.46029 |
| [a5] | B.E. Johnson, "Perturbations of multiplication and homomorphisms" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 565–579 MR0981628 Zbl 0676.46051 |
| [a6] | A. Lichnerowicz, "Applications of the deformations of algebraic structures to geometry and mathematical physics" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 855–896 MR981634 Zbl 0674.58021 |
| [a7] | F. Bayen, M. Flato, C. Fronsdal, A. Lichnerowicz, D. Sternheimer, "Deformation theory and quantization" Ann. of Physics , 111 (1978) pp. 61–110; 111–151 MR0496158 MR0496157 Zbl 0377.53025 Zbl 0377.53024 |
| [a8] | M. de Wilde, P. Lecomte, "Invariant deformations of the Poisson Lie algebra of a symplectic manifold and star-products" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 897–960 |
| [a9] | M. Goze, "Perturbations of Lie algebra structures" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 265–356 MR0981620 Zbl 0715.17009 |
| [a10] | J.M. Ancochea Bermudez, "On the rigidity of solvable Lie algebras" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 403–446 Zbl 0672.17006 |
| [a11] | D.G. Babbitt, V.S. Varadarajan, "Local isoformal deformation theory for meromorphic differential equations near an irregular singularity" M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) pp. 583–700 MR0981629 Zbl 0668.34010 |
| [a12] | M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) MR0981617 Zbl 0654.00006 |
| [a13] | D. Sternheimer, "Star products: their ubiquity and unicity" J. Bertrand (ed.) et al. (ed.) , Modern Group Theoretical Methods in Physics: Proc. Conf. in Honour of Guy Rideau , Kluwer (1995) pp. 255–265 MR1361453 Zbl 0905.17026 |
| [a14] | A. Weinstein, "Deformation quantization" Sem. Bourbaki , 789 (1994) MR2341828 MR1480730 MR1321655 Zbl 1146.53072 Zbl 1166.53324 Zbl 0854.58026 |
| [a15] | A. Connes, "Noncommutative geometry" , Acad. Press (1994) MR1303779 Zbl 0818.46076 |
| [a16] | P. Deligne, "Déformations de l'algèbre des fonctions d'une variété symplectique: comparaison entre Fedosov et De Wilde, Lecomte" Selecta Math. , 1 (1995) pp. 667–697 MR1383583 |
| [a17] | B. Fedosov, "Deformation quantization and index theory" , Akademie Verlag (1996) (Translated from Russian) MR1376365 Zbl 0867.58061 |
| [a18] | M. Flato, D. Sternheimer, "Star-products, quantum groups, cyclic cohomology and pseudo-differential calculus" P. Sally (ed.) et al. (ed.) , Amer. Math. Soc. Contemp. Math. , 175 (1994) pp. 53–72 MR1302012 |
| [a19] | M. Flato, "Deformation view of physical theories" Czechoslovak J. Phys. , B32 (1982) pp. 472–475 |
A deformation of a subset $4$ of a space $x$ is a homotopy
\begin{equation} D ; A \times I \rightarrow X \end{equation}
for which $D ( \alpha , 0 ) = \alpha$ if $x \in A$. If, in addition, the set $D ( A \times I )$ belongs to some subspace $X _ { 1 }$ of $x$, $\Omega$ is said to be a deformation of $4$ in $X _ { 1 }$, and $4$ is said to be deformable in $X _ { 1 }$ in $x$. A space $x$ is said to be deformable into a subspace $X _ { 1 }$ if it is deformable in itself in $X _ { 1 }$. In particular, $x$ is contractible if and only if it is deformable in one of its points. A space $x$ is deformable into a subspace $X _ { 1 }$ if and only if for the imbedding $i : X _ { 1 } \rightarrow X$ the right homotopy inverse mapping $r : X \rightarrow X _ { 1 }$ exists, i.e. $i \circ r \sim 1$. The concept of deformation of any space in itself in a subspace is related to the concept of a weak retraction.
M.I. Voitsekhovskii
Maximilian Janisch/latexlist/Algebraic Groups/Deformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Deformation&oldid=43996