An infinite tower of non-linear evolution equations that derives its name from the simplest non-trivial system of equations contained in it, the AKNS-equations
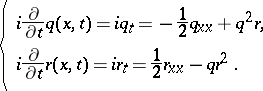 | (a1) |
It were M.J. Ablowitz, D.J. Kaup, A.C. Newell, and H. Segur who showed that the initial value problem of this system of equations (cf. also Differential equation, partial, discontinuous initial (boundary) conditions) could be solved with the inverse scattering transform (cf. also Korteweg–de Vries equation). To get a natural embedding of the AKNS-equations in a larger system, one rewrites (a1) in zero-curvature form as
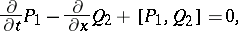 | (a2) |
where
Consider now the following polynomial expressions in the parameter  :
:
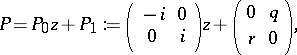 | (a3) |
where the 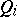 are
are 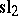 -valued functions depending on the variables
-valued functions depending on the variables  ,
,  , and
, and 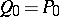 and
and 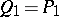 . For these data the zero-curvature equations read
. For these data the zero-curvature equations read
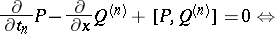 | (a4) |
which is an infinite tower of equations extending the system (a1). The system (a4) generalizes from 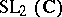 to a general simple complex Lie algebra
to a general simple complex Lie algebra 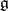 , a regular element
, a regular element 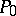 in a Cartan subalgebra
in a Cartan subalgebra 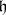 of
of 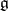 and an element
and an element 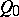 in
in 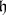 , see [a4] and [a10]. Solutions of the equations (a4) can be obtained by the Zakharov–Shabat dressing method (cf. also Soliton). Namely, consider the function
, see [a4] and [a10]. Solutions of the equations (a4) can be obtained by the Zakharov–Shabat dressing method (cf. also Soliton). Namely, consider the function
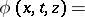 | (a5) |
with 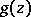 belonging to the loop group
belonging to the loop group 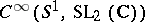 . If this
. If this 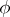 factorizes as
factorizes as 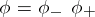 , with
, with
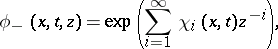 | (a6) |
then conjugating the trivial connections (cf. also Connections on a manifold) 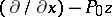 and
and 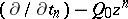 with
with 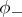 gives connections of the required form:
gives connections of the required form:
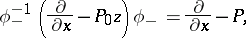 | (a7) |
Since flatness is preserved by this procedure, this leads to solutions of (a4). If 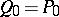 , as in the AKNS-case, one can take just as well
, as in the AKNS-case, one can take just as well 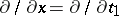 .
.
It was observed by H. Flaschka, Newell and T. Ratiu [a5] that the equations (a4) for the 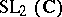 -case could be captured in the system
-case could be captured in the system
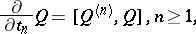 | (a8) |
for the single series
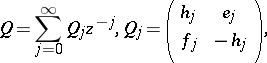 | (a9) |
They showed that these equations are commuting Hamiltonian flows (cf. also Hamiltonian system) on the Lie algebra  ,
,  , with respect to natural Poisson brackets. Further, they introduced the flux tensor
, with respect to natural Poisson brackets. Further, they introduced the flux tensor 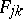 by
by
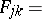 | (a10) |
and proved the local conservation laws of the system, namely
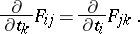 | (a11) |
The left-hand side of (a11) is, in fact, even symmetric under permutations of the indices 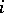 ,
, 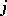 ,
, 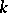 and this property made them introduce a potential
and this property made them introduce a potential  by
by
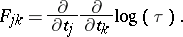 | (a12) |
The equations (a8) are called the Lax equations of the AKNS-hierarchy. As such, the AKNS-hierarchy is a natural reduction of the two-component KP-hierarchy (cf. also KP-equation; [a7]), a fact that enables a description in the Grassmannian of that hierarchy.
It was shown by M.J. Bergvelt and A.P.E. ten Kroode [a1] that it is natural to consider a system of zero-curvature relations (a4) labelled by the root lattice of the Lie algebra, where the operators at different sites of the lattice are linked by Toda-type differential-difference equations. For example, for nearest neighbour sites there holds
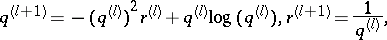 | (a13) |
where
This phenomenon is due to the fact that there is a natural lattice group that commutes with the commuting flows corresponding to the parameters 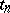 .
.
In the representation-theoretic approach to soliton equations (see [a3], [a8]), the soliton equations occur as the equations describing the group orbit of the highest weight vector. A similar description holds for these combined differential-difference equations. Let 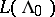 be the basic representation of the Kac–Moody Lie algebra
be the basic representation of the Kac–Moody Lie algebra 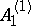 (cf. also Kac–Moody algebra). In
(cf. also Kac–Moody algebra). In 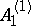 one takes the homogeneous Heisenberg algebra
one takes the homogeneous Heisenberg algebra
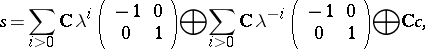 |
where  is the central element of
is the central element of 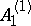 that is in the kernel of the projection of
that is in the kernel of the projection of 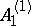 onto the loop algebra of
onto the loop algebra of 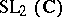 . The
. The 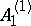 -module
-module 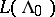 decomposes with respect to the action of the homogeneous Heisenberg algebra
decomposes with respect to the action of the homogeneous Heisenberg algebra  as a direct sum of irreducible
as a direct sum of irreducible  -modules
-modules  labelled by the root lattice. Thus, one can write each element of
labelled by the root lattice. Thus, one can write each element of  as
as 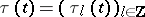 . The group orbit of the highest weight vector can then be characterized by a set of so-called Hirota bilinear relations for the components
. The group orbit of the highest weight vector can then be characterized by a set of so-called Hirota bilinear relations for the components 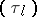 . By using the representation theory one constructs a series of elements
. By using the representation theory one constructs a series of elements 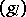 in a suitable completion of the Kac–Moody group associated with
in a suitable completion of the Kac–Moody group associated with 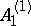 such that the vacuum expectation value of
such that the vacuum expectation value of 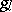 is exactly
is exactly 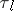 . The Birkhoff decomposition of the
. The Birkhoff decomposition of the 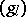 in that group then enables one to construct solutions of the lattice zero-curvature equations, [a2]. In particular, the operators
in that group then enables one to construct solutions of the lattice zero-curvature equations, [a2]. In particular, the operators 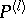 from (a13) obtained in this way can be expressed in the components
from (a13) obtained in this way can be expressed in the components 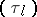 by
by
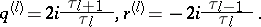 | (a14) |
By using the adjoint action of the Kac–Moody group, Bergvelt and ten Kroode also showed [a2] that the
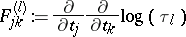 | (a15) |
give exactly the flux tensor from (a10), thus furnishing a representation-theoretic basis for the results in [a5].
A geometric way to look at  -functions, see e.g. [a9], is to consider a homogeneous space over the relevant loop group
-functions, see e.g. [a9], is to consider a homogeneous space over the relevant loop group 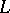 , a holomorphic line bundle
, a holomorphic line bundle 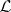 over this space and its pull-back over the corresponding central extension
over this space and its pull-back over the corresponding central extension 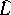 of
of 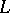 . If this last line bundle has a global holomorphic section, then
. If this last line bundle has a global holomorphic section, then  -functions measure the failure of equivariance of partial liftings from
-functions measure the failure of equivariance of partial liftings from 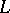 to
to 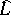 with respect to this section. With this point of view, one can also arrive at the formulas in (a14) by lifting the discrete group of transformations that commute with the flows from (a6) appropriately, see [a11].
with respect to this section. With this point of view, one can also arrive at the formulas in (a14) by lifting the discrete group of transformations that commute with the flows from (a6) appropriately, see [a11].
An important class of equations associated with the AKNS-hierarchy are the so-called stationary AKNS-equations. These are the differential equations for the functions 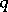 and
and  from the first-order differential operator
from the first-order differential operator
resulting from the existence of a 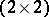 -matrix-valued differential operator
-matrix-valued differential operator
that commutes with 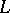 . Such a pair is naturally associated with a hyper-elliptic curve of genus
. Such a pair is naturally associated with a hyper-elliptic curve of genus  and that is why one calls
and that is why one calls 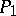 an algebro-geometric AKNS-potential. The elliptic algebro-geometric AKNS-potentials have been characterized in [a6]. They correspond exactly to the potentials for which the equation
an algebro-geometric AKNS-potential. The elliptic algebro-geometric AKNS-potentials have been characterized in [a6]. They correspond exactly to the potentials for which the equation 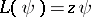 has a meromorphic fundamental system of solutions with respect to
has a meromorphic fundamental system of solutions with respect to  for all values of the spectral parameter
for all values of the spectral parameter 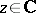 .
.
References
| [a1] | M.J. Bergvelt, A.P.E. ten Kroode, "Differential-difference  equations and homogeneous Heisenberg algebras" J. Math. Phys. , 28 (1987) pp. 302–306 equations and homogeneous Heisenberg algebras" J. Math. Phys. , 28 (1987) pp. 302–306 |
| [a2] | M.J. Bergvelt, A.P.E. ten Kroode, " -functions and zero curvature equations of Toda–AKNS type" J. Math. Phys. , 29 (1988) pp. 1308–1320 -functions and zero curvature equations of Toda–AKNS type" J. Math. Phys. , 29 (1988) pp. 1308–1320 |
| [a3] | E. Date, M. Jimbo, M. Kashiwara, T. Miwa, "Transformation groups for soliton equations" , Non-linear Integrable Systems; Classical Theory and Quantum Theory (Proc. RIMS Symp.) , World Sci. (1983) pp. 41–119 |
| [a4] | V.G. Drinfel'd, V.V. Sokolov, "Lie algebras and equations of Korteweg de Vries type" Itogi Nauki i Tekhn. Ser. Sovrem. Probl. Mat. , 24 (1984) pp. 81–180 (In Russian) |
| [a5] | H. Flaschka, A.C. Newell, T. Ratiu, "Kac–Moody Lie algebras and soliton equations II. Lax equations associated with 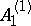 " Physica , 9D (1983) pp. 300–323 " Physica , 9D (1983) pp. 300–323 |
| [a6] | F. Gesztesy, R. Weikard, "A characterization of all elliptic algebro-geometric solutions of the AKNS hierarchy" Acta Math. , 181 (1998) pp. 63–108 |
| [a7] | G.F. Helminck, G.F. Post, "A convergent framework for the multicomponent 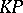 -hierarchy" Trans. Amer. Math. Soc. , 324 : 1 (1991) pp. 271–292 -hierarchy" Trans. Amer. Math. Soc. , 324 : 1 (1991) pp. 271–292 |
| [a8] | V.G. Kac, "Infinite dimensional Lie algebras" , Cambridge Univ. Press (1989) (Edition: Third) |
| [a9] | G. Segal, G. Wilson, "Loop groups and equations of KdV type" Publ. Math. IHES , 63 (1985) pp. 1–64 |
| [a10] | G. Wilson, "The modified Lax and two-dimensional Toda lattice equations associated with simple Lie algebras" Ergod. Th. Dynam. Syst. , 1 (1981) pp. 361–380 |
| [a11] | G. Wilson, "The  -functions of the AKNS equations" , Integrable Systems: the Verdier Memorial Conf. (Actes Colloq. Internat. Luminy) , Progress in Math. , 115 (1993) pp. 131–145 -functions of the AKNS equations" , Integrable Systems: the Verdier Memorial Conf. (Actes Colloq. Internat. Luminy) , Progress in Math. , 115 (1993) pp. 131–145 |
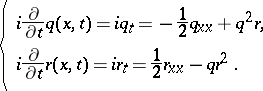
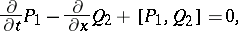

 :
:
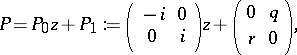
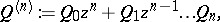
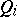 are
are 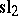 -valued functions depending on the variables
-valued functions depending on the variables  ,
,  , and
, and 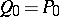 and
and 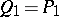 . For these data the zero-curvature equations read
. For these data the zero-curvature equations read
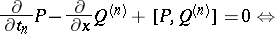
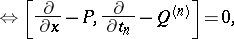
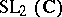 to a general simple complex Lie algebra
to a general simple complex Lie algebra 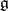 , a regular element
, a regular element 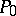 in a Cartan subalgebra
in a Cartan subalgebra 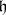 of
of 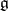 and an element
and an element 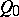 in
in 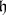 , see [a4] and [a10]. Solutions of the equations (a4) can be obtained by the Zakharov–Shabat dressing method (cf. also Soliton). Namely, consider the function
, see [a4] and [a10]. Solutions of the equations (a4) can be obtained by the Zakharov–Shabat dressing method (cf. also Soliton). Namely, consider the function
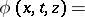
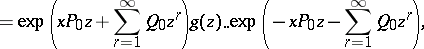
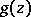 belonging to the loop group
belonging to the loop group 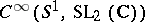 . If this
. If this 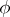 factorizes as
factorizes as 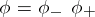 , with
, with
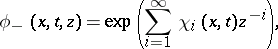
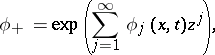
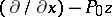 and
and 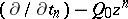 with
with 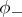 gives connections of the required form:
gives connections of the required form:
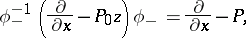
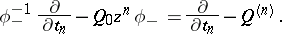
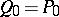 , as in the AKNS-case, one can take just as well
, as in the AKNS-case, one can take just as well 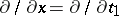 .
.
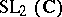 -case could be captured in the system
-case could be captured in the system
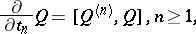
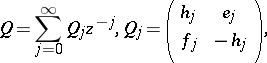
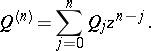
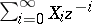 ,
, 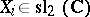 , with respect to natural Poisson brackets. Further, they introduced the flux tensor
, with respect to natural Poisson brackets. Further, they introduced the flux tensor 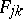 by
by
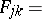
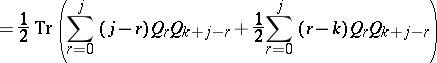
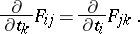
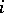 ,
, 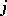 ,
, 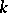 and this property made them introduce a potential
and this property made them introduce a potential  by
by
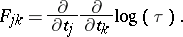
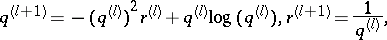
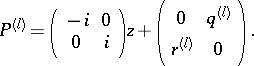
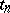 .
.
 be the basic representation of the Kac–Moody Lie algebra
be the basic representation of the Kac–Moody Lie algebra 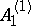 (cf. also Kac–Moody algebra). In
(cf. also Kac–Moody algebra). In 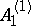 one takes the homogeneous Heisenberg algebra
one takes the homogeneous Heisenberg algebra
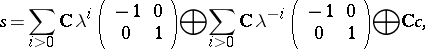
 is the central element of
is the central element of 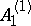 that is in the kernel of the projection of
that is in the kernel of the projection of 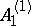 onto the loop algebra of
onto the loop algebra of 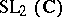 . The
. The 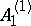 -module
-module 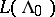 decomposes with respect to the action of the homogeneous Heisenberg algebra
decomposes with respect to the action of the homogeneous Heisenberg algebra  as a direct sum of irreducible
as a direct sum of irreducible  -modules
-modules 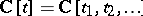 labelled by the root lattice. Thus, one can write each element of
labelled by the root lattice. Thus, one can write each element of 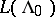 as
as 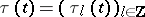 . The group orbit of the highest weight vector can then be characterized by a set of so-called Hirota bilinear relations for the components
. The group orbit of the highest weight vector can then be characterized by a set of so-called Hirota bilinear relations for the components 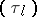 . By using the representation theory one constructs a series of elements
. By using the representation theory one constructs a series of elements 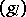 in a suitable completion of the Kac–Moody group associated with
in a suitable completion of the Kac–Moody group associated with 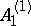 such that the vacuum expectation value of
such that the vacuum expectation value of 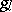 is exactly
is exactly 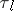 . The Birkhoff decomposition of the
. The Birkhoff decomposition of the 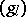 in that group then enables one to construct solutions of the lattice zero-curvature equations, [a2]. In particular, the operators
in that group then enables one to construct solutions of the lattice zero-curvature equations, [a2]. In particular, the operators 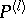 from (a13) obtained in this way can be expressed in the components
from (a13) obtained in this way can be expressed in the components 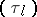 by
by
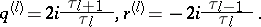
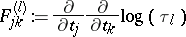
 -functions, see e.g. [a9], is to consider a homogeneous space over the relevant loop group
-functions, see e.g. [a9], is to consider a homogeneous space over the relevant loop group 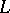 , a holomorphic line bundle
, a holomorphic line bundle 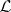 over this space and its pull-back over the corresponding central extension
over this space and its pull-back over the corresponding central extension 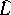 of
of 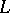 . If this last line bundle has a global holomorphic section, then
. If this last line bundle has a global holomorphic section, then  -functions measure the failure of equivariance of partial liftings from
-functions measure the failure of equivariance of partial liftings from 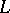 to
to 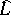 with respect to this section. With this point of view, one can also arrive at the formulas in (a14) by lifting the discrete group of transformations that commute with the flows from (a6) appropriately, see [a11].
with respect to this section. With this point of view, one can also arrive at the formulas in (a14) by lifting the discrete group of transformations that commute with the flows from (a6) appropriately, see [a11].
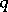 and
and  from the first-order differential operator
from the first-order differential operator

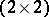 -matrix-valued differential operator
-matrix-valued differential operator
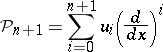
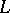 . Such a pair is naturally associated with a hyper-elliptic curve of genus
. Such a pair is naturally associated with a hyper-elliptic curve of genus  and that is why one calls
and that is why one calls 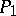 an algebro-geometric AKNS-potential. The elliptic algebro-geometric AKNS-potentials have been characterized in [a6]. They correspond exactly to the potentials for which the equation
an algebro-geometric AKNS-potential. The elliptic algebro-geometric AKNS-potentials have been characterized in [a6]. They correspond exactly to the potentials for which the equation 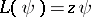 has a meromorphic fundamental system of solutions with respect to
has a meromorphic fundamental system of solutions with respect to  for all values of the spectral parameter
for all values of the spectral parameter 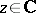 .
.
 equations and homogeneous Heisenberg algebras" J. Math. Phys. , 28 (1987) pp. 302–306
equations and homogeneous Heisenberg algebras" J. Math. Phys. , 28 (1987) pp. 302–306 -functions and zero curvature equations of Toda–AKNS type" J. Math. Phys. , 29 (1988) pp. 1308–1320
-functions and zero curvature equations of Toda–AKNS type" J. Math. Phys. , 29 (1988) pp. 1308–1320 " Physica , 9D (1983) pp. 300–323
" Physica , 9D (1983) pp. 300–323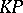 -hierarchy" Trans. Amer. Math. Soc. , 324 : 1 (1991) pp. 271–292
-hierarchy" Trans. Amer. Math. Soc. , 324 : 1 (1991) pp. 271–292 -functions of the AKNS equations" , Integrable Systems: the Verdier Memorial Conf. (Actes Colloq. Internat. Luminy) , Progress in Math. , 115 (1993) pp. 131–145
-functions of the AKNS equations" , Integrable Systems: the Verdier Memorial Conf. (Actes Colloq. Internat. Luminy) , Progress in Math. , 115 (1993) pp. 131–145