Difference between revisions of "User:Matteo.focardi/sandbox"
(Created page with "A theorem on the relation between the concepts of almost-everywhere convergence and uniform convergence of a sequence of functions. Let $\mu$ be a [[Set function|$\sigma$-ad...") |
|||
| Line 1: | Line 1: | ||
| − | A theorem on the relation between the concepts of almost-everywhere convergence and uniform convergence of a sequence of functions. Let $\mu$ be a [[Set function|$\sigma$-additive measure]] defined on a [[Algebra of sets|$\sigma$-algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e0351204.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e0351205.png" />, $\mu(E)<+\infty$, and let a sequence of $\mu$-measurable almost-everywhere finite functions $f_k(x)$, $x\in E$, $k=1,2,\ldots$, converge almost-everywhere to a function $f(x)$. Then for any $\varepsilon>0$ there exists a measurable set $E_\varepsilon\subset E$ such that $\mu(E\setminus E_\varepsilon)<\varepsilon$, and the sequence | + | {{MSC|28A}} |
| + | |||
| + | [[Category:Classical measure theory]] | ||
| + | |||
| + | {{TEX|done}} | ||
| + | |||
| + | |||
| + | A theorem on the relation between the concepts of almost-everywhere convergence and uniform convergence of a sequence of functions. Let $\mu$ be a [[Set function|$\sigma$-additive measure]] defined on a [[Algebra of sets|$\sigma$-algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e0351204.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e0351205.png" />, $\mu(E)<+\infty$, and let a sequence of $\mu$-measurable almost-everywhere finite functions $f_k(x)$, $x\in E$, $k=1,2,\ldots$, converge almost-everywhere to a function $f(x)$. Then for any $\varepsilon>0$ there exists a measurable set $E_\varepsilon\subset E$ such that $\mu(E\setminus E_\varepsilon)<\varepsilon$, and the sequence $f_k(x)$ converges to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512016.png" /> uniformly on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512017.png" />. For the case where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512018.png" /> is the Lebesgue measure on the line this was proved by D.F. Egorov [[#References|[1]]]. | ||
Egorov's theorem has various generalizations extending its potentialities. For example, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512019.png" /> be a sequence of measurable mappings of a locally compact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512020.png" /> into a metrizable space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512021.png" /> for which the limit | Egorov's theorem has various generalizations extending its potentialities. For example, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512019.png" /> be a sequence of measurable mappings of a locally compact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512020.png" /> into a metrizable space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035120/e03512021.png" /> for which the limit | ||
Revision as of 11:42, 18 October 2012
2020 Mathematics Subject Classification: Primary: 28A [MSN][ZBL]
A theorem on the relation between the concepts of almost-everywhere convergence and uniform convergence of a sequence of functions. Let $\mu$ be a $\sigma$-additive measure defined on a $\sigma$-algebra 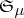 , let
, let 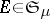 , $\mu(E)<+\infty$, and let a sequence of $\mu$-measurable almost-everywhere finite functions $f_k(x)$, $x\in E$, $k=1,2,\ldots$, converge almost-everywhere to a function $f(x)$. Then for any $\varepsilon>0$ there exists a measurable set $E_\varepsilon\subset E$ such that $\mu(E\setminus E_\varepsilon)<\varepsilon$, and the sequence $f_k(x)$ converges to
, $\mu(E)<+\infty$, and let a sequence of $\mu$-measurable almost-everywhere finite functions $f_k(x)$, $x\in E$, $k=1,2,\ldots$, converge almost-everywhere to a function $f(x)$. Then for any $\varepsilon>0$ there exists a measurable set $E_\varepsilon\subset E$ such that $\mu(E\setminus E_\varepsilon)<\varepsilon$, and the sequence $f_k(x)$ converges to 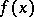 uniformly on
uniformly on  . For the case where
. For the case where 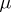 is the Lebesgue measure on the line this was proved by D.F. Egorov [1].
is the Lebesgue measure on the line this was proved by D.F. Egorov [1].
Egorov's theorem has various generalizations extending its potentialities. For example, let 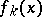 be a sequence of measurable mappings of a locally compact space
be a sequence of measurable mappings of a locally compact space  into a metrizable space
into a metrizable space 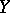 for which the limit
for which the limit
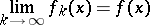 |
exists locally almost-everywhere on  with respect to a Radon measure
with respect to a Radon measure 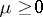 . Then
. Then 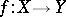 is measurable with respect to
is measurable with respect to 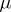 , and for any compact set
, and for any compact set 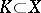 and
and 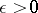 there is a compact set
there is a compact set 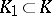 such that
such that 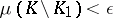 , and the restriction of
, and the restriction of 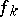 to
to 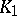 is continuous and converges to
is continuous and converges to 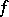 uniformly on
uniformly on 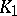 . The conclusion of Egorov's theorem may be false if
. The conclusion of Egorov's theorem may be false if  is not metrizable.
is not metrizable.
References
| [1] | D.F. Egorov, "Sur les suites de fonctions mesurables" C.R. Acad. Sci. Paris , 152 (1911) pp. 244–246 |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801 |
| [3] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) MR0583191 Zbl 1116.28002 Zbl 1106.46005 Zbl 1106.46006 Zbl 1182.28002 Zbl 1182.28001 Zbl 1095.28002 Zbl 1095.28001 Zbl 0156.06001 |
Comments
In 1970, G. Mokobodzki obtained a nice generalization of Egorov's theorem (see [a2], [a3]): Let  ,
, 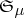 and
and 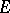 be as above. Let
be as above. Let  be a set of
be a set of 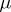 -measurable finite functions that is compact in the topology of pointwise convergence. Then there is a sequence
-measurable finite functions that is compact in the topology of pointwise convergence. Then there is a sequence 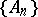 of disjoint sets belonging to
of disjoint sets belonging to 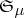 such that the support of
such that the support of 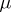 is contained in
is contained in  and such that, for every
and such that, for every  , the set
, the set 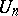 of restrictions to
of restrictions to  of the elements of
of the elements of 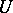 is compact in the topology of uniform convergence.
is compact in the topology of uniform convergence.
Egorov's theorem is related to the Luzin  -property.
-property.
References
| [a1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
| [a2] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , C , North-Holland (1988) (Translated from French) MR0939365 Zbl 0716.60001 |
| [a3] | D. Revuz, "Markov chains" , North-Holland (1975) MR0415773 Zbl 0332.60045 |
Matteo.focardi/sandbox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matteo.focardi/sandbox&oldid=28507