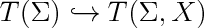|
|
| (254 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | $\newcommand{\Om}{\Omega}
| + | <ref> [http://hea-www.harvard.edu/AstroStat http://hea-www.harvard.edu/AstroStat]; <nowiki> http://www.incagroup.org </nowiki>; <nowiki> http://astrostatistics.psu.edu </nowiki> </ref> |
| − | \newcommand{\F}{\mathcal F}
| |
| − | \newcommand{\B}{\mathcal B}
| |
| − | \newcommand{\M}{\mathcal M} $
| |
| − | A [[probability space]] is called '''standard''' if it is a [[standard Borel space]] endowed with a [[probability measure]], completed with null sets, and possibly augmented with another null set. (See Definition 1 below.) Every standard probability space is isomorphic (mod 0) to an interval with [[Lebesgue measure]], a finite or countable set of atoms, or a combination of both. (See Theorem ? below.)
| |
| | | | |
| − | ''Example.'' The set of all continuous functions $[0,\infty)\to\R$ with the [[Wiener measure]] is a standard probability space.
| + | ====Notes==== |
| | + | <references /> |
| | | | |
| − | ''Non-example.'' The set $[0,1]^\R$ of all functions $\R\to[0,1]$ with the product of Lebesgue measures is a nonstandard probability space.
| + | ------------------------------------------- |
| | | | |
| − | '''Definition 1a.''' A probability space $(\Om,\F,P)$ is ''standard'' if it is [[Measure space#complete|complete]] and there exist a subset $\Om_1\subset\Om$ and a σ-field (in other words, σ-algebra) $\B$ on $\Om_1$ such that $(\Om_1,\B)$ is a standard Borel space and $\forall A\in\F \;\; \exists B\in\B \; \big( B \subset A \land P(B)=P(A) \big)$.
| |
| | | | |
| − | '''Definition 1b''' (equivalent). A probability space $(\Om,\F,P)$ is ''standard'' if it is complete, [[Measure space#perfect|perfect]] and countably separated mod 0 in the following sense: some subset of full measure, treated as a [[Measurable space#subspace|subspace]] of the measurable space $(\Om,\F)$, is a [[Measurable space#separated|countably separated]] measurable space.
| + | {| |
| | + | | A || B || C |
| | + | |- |
| | + | | X || Y || Z |
| | + | |} |
| | | | |
| | | | |
| − | -------------------------------------------------------
| |
| | | | |
| − | ====On terminology====
| + | ----------------------------------------- |
| | + | ----------------------------------------- |
| | | | |
| − | In {{Cite|M|Sect. 6}} universally measurable spaces are called metrically standard Borel spaces.
| + | $\newcommand*{\longhookrightarrow}{\lhook\joinrel\relbar\joinrel\rightarrow}$ |
| | | | |
| − | In {{Cite|K|Sect. 21.D}} universally measurable subsets of a standard (rather than arbitrary) measurable space are defined.
| + | <asy> |
| | + | size(100,100); |
| | + | label(scale(1.7)*'$T(\\Sigma)\hookrightarrow T(\\Sigma,X)$',(0,0)); |
| | + | </asy> |
| | | | |
| − | In {{Cite|N|Sect. 1.1}} an absolute measurable space is defined as a separable metrizable topological space such that every its homeomorphic image in every such space (with the Borel σ-algebra) is a universally measurable subset. The corresponding measurable space (with the Borel σ-algebra) is also called an absolute measurable space in {{Cite|N|Sect. B.2}}.
| + | <asy> |
| | + | size(220,220); |
| | | | |
| − | ====References====
| + | import math; |
| | | | |
| − | {|
| + | int kmax=40; |
| − | |valign="top"|{{Ref|I}}|| Kiyosi Itô, "Introduction to probability theory", Cambridge (1984). {{MR|0777504}} {{ZBL|0545.60001}}
| + | |
| − | |-
| + | guide g; |
| − | |valign="top"|{{Ref|C}}|| Donald L. Cohn, "Measure theory", Birkhäuser (1993). {{MR|1454121}} {{ZBL|0860.28001}}
| + | for (int k=-kmax; k<=kmax; ++k) { |
| − | |-
| + | real phi = 0.2*k*pi; |
| − | |valign="top"|{{Ref|D}}|| Richard M. Dudley, "Real analysis and probability", Wadsworth&Brooks/Cole (1989). {{MR|0982264}} {{ZBL|0686.60001}}
| + | real rho = 1; |
| − | |-
| + | if (k!=0) { |
| − | |valign="top"|{{Ref|M}}|| George W. Mackey, "Borel structure in groups and their duals", ''Trans. Amer. Math. Soc.'' '''85''' (1957), 134–165. {{MR|0089999}} {{ZBL|0082.11201}}
| + | rho = sin(phi)/phi; |
| − | |-
| + | } |
| − | |valign="top"|{{Ref|K}}|| Alexander S. Kechris, "Classical descriptive set theory", Springer-Verlag (1995). {{MR|1321597}} {{ZBL|0819.04002}}
| + | pair z=rho*expi(phi); |
| − | |-
| + | g=g..z; |
| − | |valign="top"|{{Ref|N}}|| Togo Nishiura, "Absolute measurable spaces", Cambridge (2008). {{MR|2426721}} {{ZBL|1151.54001}}
| + | } |
| − | |}
| + | |
| | + | draw (g); |
| | + | |
| | + | defaultpen(0.75); |
| | + | draw ( (0,0)--(1.3,0), dotted, Arrow(SimpleHead,5) ); |
| | + | dot ( (1,0) ); |
| | + | label ( "$a$", (1,0), NE ); |
| | + | |
| | + | </asy> |