Urysohn lemma
From Encyclopedia of Mathematics
For any two disjoint closed sets 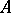 and
and 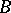 of a normal space
of a normal space 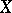 there exists a real-valued function
there exists a real-valued function 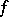 , continuous at all points, taking the value
, continuous at all points, taking the value  at all points of
at all points of 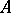 , the value 1 at all points of
, the value 1 at all points of 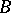 and for all
and for all 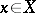 satisfying the inequality
satisfying the inequality 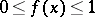 . This lemma expresses a condition which is not only necessary but also sufficient for a
. This lemma expresses a condition which is not only necessary but also sufficient for a 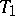 -space
-space 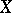 to be normal (cf. also Separation axiom; Urysohn–Brouwer lemma).
to be normal (cf. also Separation axiom; Urysohn–Brouwer lemma).
Comments
The phrase "Urysohn lemma" is sometimes also used to refer to the Urysohn metrization theorem.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) pp. 123–124 (Translated from Russian) |
| [a2] | J.L. Kelley, "General topology" , v. Nostrand (1955) pp. 115 |
How to Cite This Entry:
Urysohn lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Urysohn_lemma&oldid=15326
Urysohn lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Urysohn_lemma&oldid=15326
This article was adapted from an original article by P.S. Aleksandrov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article