Universal enveloping algebra
of a Lie algebra 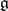 over a commutative ring
over a commutative ring 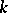 with a unit element
with a unit element
The associative 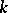 -algebra
-algebra 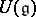 with a unit element, together with a mapping
with a unit element, together with a mapping 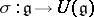 for which the following properties hold: 1)
for which the following properties hold: 1) 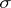 is a homomorphism of Lie algebras, i.e.
is a homomorphism of Lie algebras, i.e. 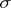 is
is 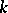 -linear and
-linear and 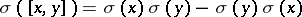 ,
,  ; 2) for every associative
; 2) for every associative 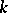 -algebra
-algebra 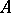 with a unit element and every
with a unit element and every 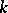 -algebra mapping
-algebra mapping 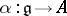 such that
such that 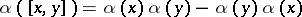 ,
, 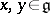 , there exists a unique homomorphism of associative algebras
, there exists a unique homomorphism of associative algebras 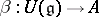 , mapping the unit to the unit, such that
, mapping the unit to the unit, such that 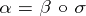 . The universal enveloping algebra is unique up to an isomorphism and always exists: If
. The universal enveloping algebra is unique up to an isomorphism and always exists: If 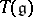 is the tensor algebra of the
is the tensor algebra of the 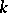 -module
-module 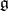 ,
, 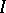 is the two-sided ideal generated by all elements of the form
is the two-sided ideal generated by all elements of the form 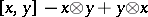 ,
, 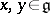 , and
, and 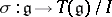 is the canonical mapping, then
is the canonical mapping, then 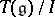 is the universal enveloping algebra of
is the universal enveloping algebra of 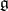 .
.
If 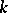 is Noetherian and the module
is Noetherian and the module 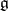 has finite order, then the algebra
has finite order, then the algebra 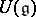 is left and right Noetherian. If
is left and right Noetherian. If 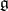 is a free module over an integral domain
is a free module over an integral domain 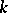 , then
, then 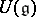 has no zero divisors. For any finite-dimensional Lie algebra
has no zero divisors. For any finite-dimensional Lie algebra 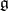 over a field
over a field 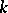 the algebra
the algebra 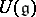 satisfies the Ore condition (cf. Imbedding of semi-groups) and so has a skew-field of fractions.
satisfies the Ore condition (cf. Imbedding of semi-groups) and so has a skew-field of fractions.
If 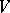 is any
is any 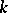 -module, then every homomorphism of Lie algebras
-module, then every homomorphism of Lie algebras 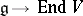 extends to a homomorphism of associative algebras
extends to a homomorphism of associative algebras 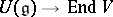 . This establishes an isomorphism of the category of
. This establishes an isomorphism of the category of 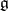 -modules and the category of left
-modules and the category of left 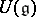 -modules, whose existence forms the basis for the application of universal enveloping algebras in the theory of representations of Lie algebras (cf. [3], [4]).
-modules, whose existence forms the basis for the application of universal enveloping algebras in the theory of representations of Lie algebras (cf. [3], [4]).
The universal enveloping algebra of the direct product of Lie algebras  is the tensor product of the algebras
is the tensor product of the algebras 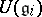 . If
. If 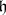 is a subalgebra of
is a subalgebra of 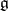 , where
, where 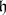 and
and 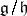 are free
are free 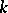 -modules, then the canonical homomorphism
-modules, then the canonical homomorphism 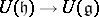 is an imbedding. If
is an imbedding. If 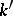 is an extension of the field
is an extension of the field 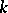 , then
, then 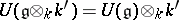 . A universal enveloping algebra has a canonical filtration
. A universal enveloping algebra has a canonical filtration 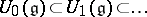 , where
, where 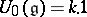 and
and 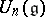 for
for 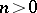 is the
is the 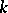 -submodule of
-submodule of 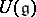 generated by the products
generated by the products 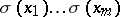 ,
, 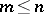 ,
,  for all
for all 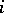 . The graded algebra
. The graded algebra 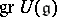 associated to this filtration is commutative and is generated by the image under the natural homomorphism
associated to this filtration is commutative and is generated by the image under the natural homomorphism  ; this mapping defines a homomorphism
; this mapping defines a homomorphism 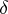 of the symmetric algebra
of the symmetric algebra 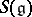 of the
of the 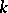 -module
-module 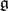 onto
onto 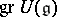 . By the Poincaré–Birkhoff–Witt theorem,
. By the Poincaré–Birkhoff–Witt theorem, 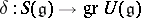 is an algebra isomorphism if
is an algebra isomorphism if 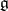 is a free
is a free 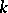 -module. The following is an equivalent formulation: If
-module. The following is an equivalent formulation: If 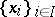 is a basis of the
is a basis of the 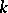 -module
-module 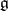 , where
, where 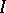 is a totally ordered set, then the family of monomials
is a totally ordered set, then the family of monomials 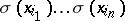 ,
, 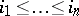 ,
, 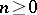 , forms a basis of the
, forms a basis of the 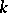 -module
-module 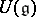 (in particular,
(in particular, 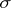 is injective).
is injective).
Let 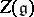 be the centre of
be the centre of 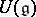 . Then for any finite-dimensional Lie algebra
. Then for any finite-dimensional Lie algebra 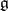 over a field of characteristic zero,
over a field of characteristic zero, 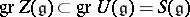 consists of the subalgebra of
consists of the subalgebra of 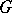 -invariant elements in
-invariant elements in 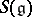 . If
. If 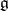 is semi-simple, then
is semi-simple, then 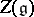 is the algebra of polynomials in
is the algebra of polynomials in  variables.
variables.
One of the important directions of research in universal enveloping algebra is the study of primitive ideals (cf. Primitive ideal; [3]).
References
| [1] | N. Bourbaki, "Lie groups and Lie algebras" , Elements of mathematics , Hermann (1975) pp. Chapts. 1–3 (Translated from French) |
| [2] | N. Bourbaki, "Groupes et algèbres de Lie" , Hermann (1975) pp. Chapts. VII-VIII |
| [3] | J. Dixmier, "Enveloping algebras" , North-Holland (1977) (Translated from French) |
| [4] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [5] | I.M. Gel'fand, "The centre of an infinitesimal group ring" Mat. Sb. , 26 (1950) pp. 103–112 (In Russian) |
| [6] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
Comments
References
| [a1] | J.C. Jantzen, "Einhüllende Algebren halbeinfacher Lie-Algebren" , Springer (1983) |
Universal enveloping algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universal_enveloping_algebra&oldid=18977