Unitary space
From Encyclopedia of Mathematics
A vector space over the field  of complex numbers, on which there is given an inner product of vectors (where the product
of complex numbers, on which there is given an inner product of vectors (where the product 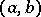 of two vectors
of two vectors  and
and  is, in general, a complex number) that satisfies the following axioms:
is, in general, a complex number) that satisfies the following axioms:
1)  ;
;
2) 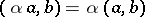 ;
;
3) 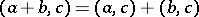 ;
;
4) if 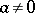 , then
, then 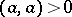 , i.e. the scalar square of a non-zero vector is a positive real number.
, i.e. the scalar square of a non-zero vector is a positive real number.
A unitary space need not be finite-dimensional. In a unitary space one can, just as in Euclidean spaces, introduce the concept of orthogonality and of an orthonormal system of vectors, and in the finite-dimensional case one can prove the existence of an orthonormal basis.
Comments
References
| [a1] | W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. 338 |
| [a2] | W.H. Greub, "Linear algebra" , Springer (1975) pp. Chapt. XI |
How to Cite This Entry:
Unitary space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_space&oldid=17853
Unitary space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_space&oldid=17853
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article