Unitary group

relative to a form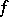

The group 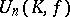of all linear transformations 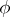of an -dimensional right linear space 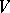over a skew-field 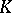, preserving a fixed non-singular sesquilinear (relative to an involuti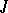on on 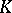) form 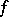on 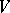, i.e. a 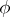such that

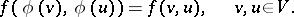A unitary group is a classical group. Particular cases of unitary groups are a symplectic group (in this case 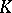is a fiel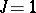d, and 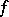is an alternating bilinear form) and an orthogonal group ( 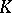is a fiel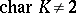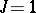d, , and 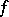is a symmetric bilinear form). Henceforth, suppose that 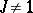and that 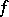possesses property 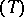(cf. Witt theorem). Multiplying by a suitable scalar, one can, without changing the unitary group, arrange that 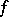is a Hermitian form, and moreover, by changing 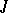, that 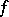is skew-Hermitian.

If one excludes the case 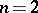, , then every element of 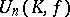can be written as a product of at most 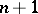pseudo-reflections (i.e. transformations fixing all elements of some non-isotropic hyperplane in 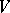). The centre 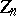of 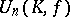consists of all homotheties of 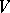of the form , , .

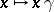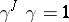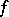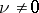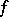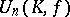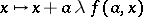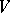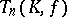Let be the Witt index of the form . If , it will be convenient to take skew-Hermitian. Let be the normal subgroup of generated by the unitary transvections, i.e. by the linear transformations of the form , where is an isotropic vector in and . The centre of the group is 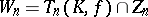. The quotient group 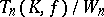is simple for 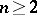, provided 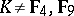. The structure of the quotient group 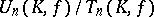may be described as follows. 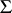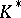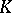Let be the subgroup of the multiplicative group of generated by 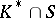and let be the subgroup of 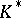generated by the elements 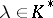with the following property: In 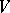there exists a hyperbolic plane (i.e. a non-isotropic two-dimensional subspace containing an isotropic vector) such that 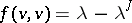for a certain vector 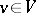orthogonal to the given plane. This subgroup is normal in 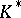. 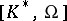Let be the subgroup of 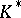generated by the commutators 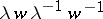, , 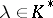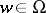. If one excludes the case 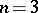, , 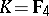then 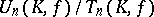is isomorphic to 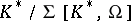for .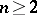

In many cases the group 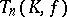coincides with the commutator subgroup of 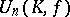; this is true, for example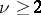, if . If 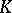is commutative and 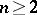, then 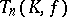coincides with the normal subgroup 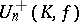of all elements with Dieudonné determinant (cf. Determinant) equal to 1 (excluding the case 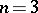, 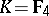). The relation between and 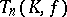has also been studied in the case when the skew-field 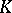is finite dimensional over its centre [1].

Suppose now that 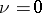. Then many of the stated results no longer hold (there are examples of unitary groups having an infinite series of normal subgroups with Abelian factors, examples of unitary groups for which 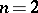and 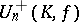does not coincide with the commutator subgroup, etc.). The case most studied is that of locally compact skew-fields of characteristic 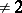and algebraic number fields.

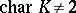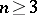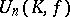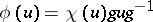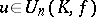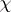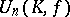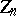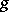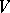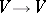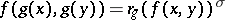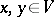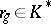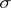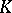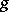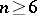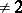One of the basic results on automorphisms of unitary groups is the following (cf. [1]): If and , then every automorphism of the unitary group has the form , , where is a homomorphism of into its centre and a unitary semi-similitude of (i.e. a bijective semi-linear mapping satisfying the condition , where , and is the automorphism of associated with ). If is even, , is a field of characteristic and 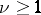, then every automorphism of 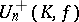is induced by an automorphism of .

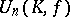If 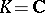, 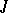is the automorphism of complex conjugation and the Hermitian form 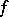is positive definite, then the unitary group 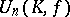is denoted by 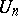; it is a real compact connected Lie group and is often simply called the unitary group. In the case of an indefinite form 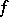the group 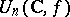is often called pseudo-unitary. By the choice of a basis in 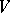, 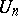may be identified with the group of all unitary matrices (cf. Unitary matrix). In that case the group 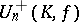is called the special unitary group and is denoted by .

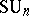References

[1]	J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1963)
[2]	N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1952–1959) pp. Chapts. 7–9
[3]	J. Dieudonné, "On the automorphisms of the classical groups" Mem. Amer. Math. Soc. , 2 (1951)
[4]	H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946)
[5]	, Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Univ. Paris (1955)
[6]	A.E. Zalesskii, "Linear groups" Russian Math. Surveys , 36 : 5 (1981) pp. 63–128 Uspekhi Mat. Nauk , 36 : 5 (1981) pp. 57–107