Unitarily-equivalent operators
Linear operators  and
and  , acting in a Hilbert space, with domains of definition
, acting in a Hilbert space, with domains of definition  and
and  , respectively, such that: 1)
, respectively, such that: 1)  ; and 2)
; and 2)  for any
for any  , where
, where  is a unitary operator. If
is a unitary operator. If  and
and  are bounded linear operators, then 1) may be omitted. If
are bounded linear operators, then 1) may be omitted. If  is a self-adjoint operator, then so is
is a self-adjoint operator, then so is 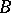 ; if
; if 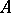 and
and  are bounded operators, then
are bounded operators, then  .
.
Self-adjoint unitarily-equivalent operators have unitarily-equivalent spectral functions, i.e. 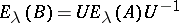 . Therefore the spectra of unitarily-equivalent operators have identical structures: either both are pure point spectra, or both are purely continuous or both are mixed. In particular, in the case of a pure point spectrum the eigenvalues of unitarily-equivalent operators are identical and the multiplicities of corresponding eigenvalues coincide; moreover, this is not only a necessary but also a sufficient condition for the unitary equivalence of operators with a pure point spectrum.
. Therefore the spectra of unitarily-equivalent operators have identical structures: either both are pure point spectra, or both are purely continuous or both are mixed. In particular, in the case of a pure point spectrum the eigenvalues of unitarily-equivalent operators are identical and the multiplicities of corresponding eigenvalues coincide; moreover, this is not only a necessary but also a sufficient condition for the unitary equivalence of operators with a pure point spectrum.
Examples of pairs of unitarily-equivalent operators in the complex space  are the differentiation operator
are the differentiation operator 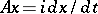 , with domain of definition
, with domain of definition 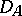 consisting of all functions that are absolutely continuous on
consisting of all functions that are absolutely continuous on  and that have a square-summable derivative in this interval, and the operator of multiplication by the independent variable,
and that have a square-summable derivative in this interval, and the operator of multiplication by the independent variable,  . In this case the unitary operator accomplishing the unitary equivalence is the Fourier transform.
. In this case the unitary operator accomplishing the unitary equivalence is the Fourier transform.
References
| [1] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
| [2] | L.A. [L.A. Lyusternik] Liusternik, "Elements of functional analysis" , F. Ungar (1961) (Translated from Russian) |
| [3] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
Comments
For non-self-adjoint operators, characteristic operator-functions provide a tool to identify classes of unitarily-equivalent operators. See [3] and [a1].
References
| [a1] | M.S. Brodskii, "Triangular and Jordan representations of linear operators" , Amer. Math. Soc. (1971) (Translated from Russian) |
Unitarily-equivalent operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitarily-equivalent_operators&oldid=11796