Uniform topology
From Encyclopedia of Mathematics
The topology generated by a uniform structure. In more detail, let  be a set equipped with a uniform structure (that is, a uniform space)
be a set equipped with a uniform structure (that is, a uniform space)  , and for each
, and for each  let
let  denote the set of subsets
denote the set of subsets  of
of  as
as  runs through the entourages of
runs through the entourages of  . Then there is in
. Then there is in 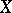 one, and moreover only one, topology (called the uniform topology) for which
one, and moreover only one, topology (called the uniform topology) for which  is the neighbourhood filter at
is the neighbourhood filter at  for any
for any 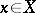 . A topology is called uniformizable if there is a uniform structure that generates it. Not every topological space is uniformizable; for example, non-regular spaces.
. A topology is called uniformizable if there is a uniform structure that generates it. Not every topological space is uniformizable; for example, non-regular spaces.
Comments
For references see Uniform space.
How to Cite This Entry:
Uniform topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_topology&oldid=16188
Uniform topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_topology&oldid=16188
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article