Uniform stability
Lyapunov stability, uniform with respect to the initial time. A solution 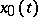 ,
, 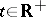 , of a system of differential equations
, of a system of differential equations
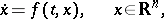 |
is called uniformly stable if for every 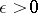 there is a
there is a 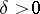 such that for every
such that for every 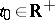 and every solution
and every solution 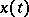 of the system satisfying the inequality
of the system satisfying the inequality
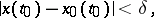 |
the inequality
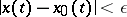 |
holds for all 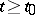 .
.
A Lyapunov-stable fixed point of an autonomous system of differential equations 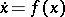 ,
,  , is uniformly stable, but, in general, a Lyapunov-stable solution need not be uniformly stable. For example, the solution
, is uniformly stable, but, in general, a Lyapunov-stable solution need not be uniformly stable. For example, the solution 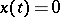 ,
, 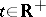 , of the equation
, of the equation
 | (1) |
is stable for each 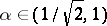 but is not uniformly stable for such
but is not uniformly stable for such 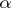 .
.
Suppose one is given a linear system of differential equations
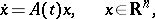 | (2) |
where 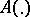 is a mapping
is a mapping 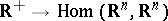 that is summable on each interval.
that is summable on each interval.
In order that the solution 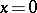 of (2) be uniformly stable, it is necessary that the upper singular exponent
of (2) be uniformly stable, it is necessary that the upper singular exponent 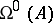 of (2) be less than or equal to zero (cf. also Singular exponents). For example, in the case of equation (1), the upper singular exponent
of (2) be less than or equal to zero (cf. also Singular exponents). For example, in the case of equation (1), the upper singular exponent 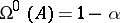 , and the Lyapunov characteristic exponent
, and the Lyapunov characteristic exponent  . For the existence of a
. For the existence of a 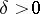 such that the solution
such that the solution 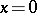 of any system
of any system
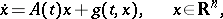 |
that satisfies the conditions of the existence and uniqueness theorem for the solution of the Cauchy problem as well as the condition
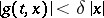 |
be uniformly stable, it is necessary and sufficient that the upper singular exponent 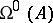 be less than zero.
be less than zero.
References
| [1] | K. Persidskii, "On stability of motion in a first approximation" Mat. Sb. , 40 : 3 (1933) pp. 284–293 (In Russian) |
| [2] | B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian) |
| [3] | Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
Comments
The upper singular exponent is also called the Bohl exponent, cf. also Singular exponents.
References
| [a1] | N. Rouché, "Stability theory by Liapunov's direct method" , Springer (1977) |
| [a2] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
| [a3] | W.A. Coppel, "Stability and asymptotic behavior of differential equations" , D.C. Heath (1965) |
Uniform stability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_stability&oldid=17527