Uniform space
A set with a uniform structure defined on it. A uniform structure (a uniformity) on a space 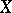 is defined by the specification of a system
is defined by the specification of a system 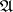 of subsets of the product
of subsets of the product 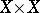 . Here the system
. Here the system  must be a filter (that is, for any
must be a filter (that is, for any 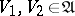 the intersection
the intersection 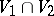 is also contained in
is also contained in 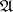 , and if
, and if 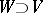 ,
,  , then
, then 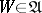 ) and must satisfy the following axioms:
) and must satisfy the following axioms:
U1) every set 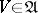 contains the diagonal
contains the diagonal 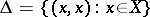 ;
;
U2) if 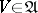 , then
, then 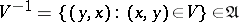 ;
;
U3) for any 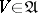 there is a
there is a 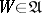 such that
such that 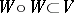 , where
, where  .
.
The elements of 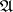 are called entourages of the uniformity defined by
are called entourages of the uniformity defined by 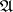 .
.
A uniformity on a set 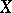 can also be defined by the specification of a system of coverings
can also be defined by the specification of a system of coverings 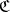 on
on 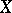 satisfying the following axioms:
satisfying the following axioms:
C1) if 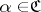 and
and 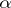 refines a covering
refines a covering 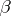 , then
, then 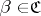 ;
;
C2) for any 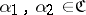 there is a covering
there is a covering 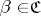 that star-refines both
that star-refines both 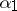 and
and 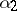 (that is, for any
(that is, for any 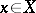 all elements of
all elements of 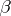 containing
containing  ly in certain elements of
ly in certain elements of 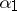 and
and 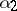 ).
).
Coverings that belong to 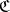 are called uniform coverings of
are called uniform coverings of 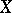 (relative to the uniformity defined by
(relative to the uniformity defined by 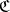 ).
).
These two methods of specifying a uniform structure are equivalent. For example, if the uniform structure on 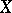 is given by a system of entourages
is given by a system of entourages 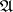 , then a system of uniform coverings
, then a system of uniform coverings  of
of 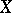 can be constructed as follows. For each
can be constructed as follows. For each 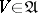 the family
the family 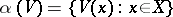 (where
(where 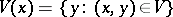 ) is a covering of
) is a covering of 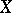 . A covering
. A covering 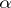 belongs to
belongs to 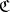 if and only if
if and only if 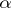 can be refined by a covering of the form
can be refined by a covering of the form 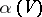 ,
,  . Conversely, if
. Conversely, if 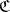 is a system of uniform coverings of a uniform space, a system of entourages is formed by the sets of the form
is a system of uniform coverings of a uniform space, a system of entourages is formed by the sets of the form 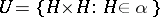 ,
,  , and all the sets containing them.
, and all the sets containing them.
A uniform structure on 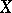 can also be given via a system of pseudo-metrics (cf. Pseudo-metric). Every uniformity on a set
can also be given via a system of pseudo-metrics (cf. Pseudo-metric). Every uniformity on a set 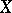 generates a topology
generates a topology 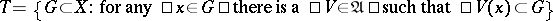 .
.
The properties of uniform spaces are generalizations of the uniform properties of metric spaces (cf. Metric space). If 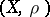 is a metric space, then on
is a metric space, then on 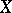 there is a uniformity generated by the metric
there is a uniformity generated by the metric  . A system of entourages for this uniformity is formed by all sets containing sets of the form
. A system of entourages for this uniformity is formed by all sets containing sets of the form 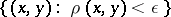 ,
, 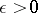 . Here the topologies on
. Here the topologies on 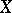 induced by the metric and the uniformity coincide. Uniform structures generated by metrics are called metrizable.
induced by the metric and the uniformity coincide. Uniform structures generated by metrics are called metrizable.
Uniform spaces were introduced in 1937 by A. Weil [1] (by means of entourages; the definition of uniform spaces by means of uniform coverings was given in 1940, see [4]). However, the idea of the use of multiple star-refinement for the construction of functions appeared earlier with L.S. Pontryagin (see [5]) (afterwards this idea was used in the proof of complete regularity of the topology of a separable uniform space). Initially, uniform spaces were used as tools for the study of the topologies (generated by them) (similar to the way a metric on a metrizable space was often used for the study of the topological properties of the space). However, the theory of uniform spaces is of independent interest, although closely connected with the theory of topological spaces.
A mapping 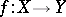 from a uniform space
from a uniform space  into a uniform space
into a uniform space 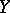 is called uniformly continuous if for any uniform covering
is called uniformly continuous if for any uniform covering 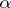 of
of 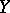 the system
the system  is a uniform covering of
is a uniform covering of  . Every uniformly-continuous mapping is continuous relative to the topologies generated by the uniform structures on
. Every uniformly-continuous mapping is continuous relative to the topologies generated by the uniform structures on 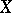 and
and 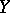 . If the uniform structures on
. If the uniform structures on  and
and 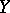 are induced by metrics, then a uniformly-continuous mapping
are induced by metrics, then a uniformly-continuous mapping 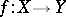 turns out to be uniformly continuous in the classical sense as a mapping between metric spaces (cf. Uniform continuity).
turns out to be uniformly continuous in the classical sense as a mapping between metric spaces (cf. Uniform continuity).
Of more interest is the theory of uniform spaces that satisfy the additional axiom of separation:
U4) 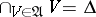 (in terms of entourages), or
(in terms of entourages), or
C3) for any two points 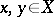 ,
, 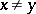 , there is an
, there is an 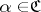 such that no element of
such that no element of  simultaneously contains
simultaneously contains  and
and 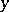 (in terms of uniform coverings).
(in terms of uniform coverings).
From now on only uniform spaces equipped with a separating uniform structure will be considered. The topology on 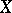 generated by a separating uniformity is completely regular and, conversely, every completely-regular topology on
generated by a separating uniformity is completely regular and, conversely, every completely-regular topology on 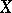 is generated by some separating uniform structure. As a rule, there are many different uniformities generating the same topology on
is generated by some separating uniform structure. As a rule, there are many different uniformities generating the same topology on 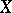 . In particular, a metrizable topology can be generated by a non-metrizable separating uniformity.
. In particular, a metrizable topology can be generated by a non-metrizable separating uniformity.
A uniform space 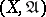 is metrizable if and only if
is metrizable if and only if 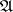 has a countable base. Here, a base of a uniformity is (in terms of entourages) any subsystem
has a countable base. Here, a base of a uniformity is (in terms of entourages) any subsystem 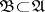 satisfying the condition: For any
satisfying the condition: For any 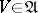 there is a
there is a 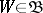 such that
such that 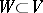 , or (in terms of uniform coverings) a subsystem
, or (in terms of uniform coverings) a subsystem 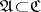 such that for any
such that for any 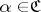 there is a
there is a 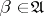 that refines
that refines 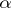 . The weight of a uniform space
. The weight of a uniform space 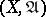 is the least cardinality of a base of the uniformity
is the least cardinality of a base of the uniformity 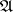 .
.
Let 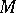 be a subset of a uniform space
be a subset of a uniform space  . The system of entourages
. The system of entourages 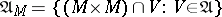 defines a uniformity on
defines a uniformity on 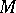 . The pair
. The pair 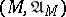 is called a subspace of
is called a subspace of 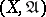 . A mapping
. A mapping 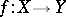 from a uniform space
from a uniform space 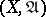 into a uniform space
into a uniform space 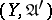 is called a uniform imbedding if
is called a uniform imbedding if 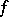 is one-to-one and uniformly continuous and if
is one-to-one and uniformly continuous and if 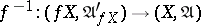 is also uniformly continuous.
is also uniformly continuous.
A uniform space 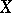 is called complete if every Cauchy filter in
is called complete if every Cauchy filter in 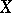 (that is a filter containing some element of each uniform covering) has a cluster point (that is, a point lying in the intersection of the closures of the elements of the filter). A metrizable uniform space is complete if and only if the metric generating its uniformity is complete. Any uniform space
(that is a filter containing some element of each uniform covering) has a cluster point (that is, a point lying in the intersection of the closures of the elements of the filter). A metrizable uniform space is complete if and only if the metric generating its uniformity is complete. Any uniform space 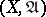 can be uniformly imbedded as an everywhere-dense subset in a unique (up to a uniform isomorphism) complete uniform space
can be uniformly imbedded as an everywhere-dense subset in a unique (up to a uniform isomorphism) complete uniform space  , which is called the completion of
, which is called the completion of 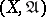 . The topology of the completion
. The topology of the completion 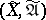 of a uniform space
of a uniform space 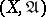 is compact if and only if
is compact if and only if 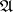 is a pre-compact uniformity (that is, such that any uniform covering refines to a finite uniform covering). In this case the space
is a pre-compact uniformity (that is, such that any uniform covering refines to a finite uniform covering). In this case the space 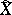 is a compactification of
is a compactification of 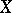 and is called the Samuel extension of
and is called the Samuel extension of 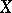 relative to the uniformity
relative to the uniformity  . For each compactification
. For each compactification 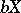 of
of 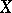 there is a unique pre-compact uniformity on
there is a unique pre-compact uniformity on 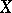 whose Samuel extension coincides with
whose Samuel extension coincides with  . Thus, all compactifications can be described in the language of pre-compact uniformities. On a compact space there is a unique uniformity (complete and pre-compact).
. Thus, all compactifications can be described in the language of pre-compact uniformities. On a compact space there is a unique uniformity (complete and pre-compact).
Every uniformity  on a set
on a set 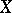 induces a proximity
induces a proximity 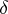 by the following formula:
by the following formula:
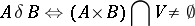 |
for all 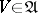 . Here the topologies generated on
. Here the topologies generated on 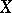 by the uniformity
by the uniformity 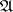 and the proximity
and the proximity 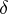 coincide. Any uniformly-continuous mapping is proximity continuous relative to the proximities generated by the uniformities. As a rule, there are many different uniformities generating the same proximity on
coincide. Any uniformly-continuous mapping is proximity continuous relative to the proximities generated by the uniformities. As a rule, there are many different uniformities generating the same proximity on 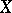 . By the same token, the set of uniformities on
. By the same token, the set of uniformities on 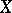 decomposes into equivalence classes (two uniformities are equivalent if the proximities they induce coincide). Each equivalence class of uniformities contains precisely one pre-compact uniformity; moreover, the Samuel extensions relative to these uniformities coincide with the Smirnov extensions (see Proximity space) relative to the proximity induced by the uniformities of the class. There is a natural partial order on the set of uniformities on
decomposes into equivalence classes (two uniformities are equivalent if the proximities they induce coincide). Each equivalence class of uniformities contains precisely one pre-compact uniformity; moreover, the Samuel extensions relative to these uniformities coincide with the Smirnov extensions (see Proximity space) relative to the proximity induced by the uniformities of the class. There is a natural partial order on the set of uniformities on 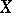 :
: 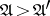 if
if 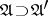 . Among all uniformities on
. Among all uniformities on 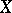 generating a fixed topology there is a largest, the so-called universal uniformity. It induces the Stone–Čech proximity on
generating a fixed topology there is a largest, the so-called universal uniformity. It induces the Stone–Čech proximity on 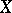 . Every pre-compact uniformity is the smallest element in its equivalence class. If
. Every pre-compact uniformity is the smallest element in its equivalence class. If 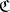 is the system of uniform coverings of some uniformity on
is the system of uniform coverings of some uniformity on 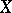 , then the system of uniform coverings of the equivalent pre-compact uniformity consists of those coverings of
, then the system of uniform coverings of the equivalent pre-compact uniformity consists of those coverings of 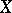 that refine a finite covering from
that refine a finite covering from 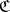 .
.
The product of uniform spaces 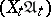 ,
, 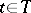 , is the uniform space
, is the uniform space 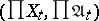 , where
, where 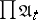 is the uniformity on
is the uniformity on  with as base for the entourages sets of the form
with as base for the entourages sets of the form
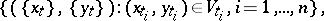 |
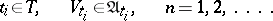 |
The topology induced on 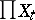 by the uniformity
by the uniformity 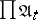 coincides with the Tikhonov product of the topologies of the spaces
coincides with the Tikhonov product of the topologies of the spaces 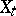 . The projections of the product onto the components are uniformly continuous. Every uniform space of weight
. The projections of the product onto the components are uniformly continuous. Every uniform space of weight  can be imbedded in a product of
can be imbedded in a product of  copies of a metrizable uniform space.
copies of a metrizable uniform space.
A family 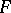 of continuous mappings from a topological space
of continuous mappings from a topological space 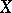 into a uniform space
into a uniform space 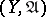 is called equicontinuous (relative to the uniformity
is called equicontinuous (relative to the uniformity 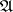 ) if for any
) if for any 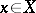 and any
and any 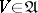 there is a neighbourhood
there is a neighbourhood 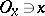 such that
such that 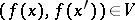 for
for 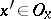 and
and 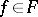 . The following generalization of the classical Ascoli theorem holds: Let
. The following generalization of the classical Ascoli theorem holds: Let 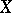 be a
be a 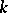 -space,
-space, 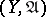 a uniform space and
a uniform space and 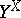 the space of continuous mappings of
the space of continuous mappings of 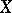 into
into 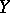 with the compact-open topology. In order that a closed subset
with the compact-open topology. In order that a closed subset  be compact it is necessary and sufficient that
be compact it is necessary and sufficient that 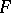 be equicontinuous relative to the uniformity
be equicontinuous relative to the uniformity 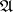 and that all sets
and that all sets  ,
, 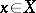 , have compact closure in
, have compact closure in  . (A
. (A 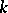 -space is a Hausdorff space that is a quotient image of a locally compact space; the class of
-space is a Hausdorff space that is a quotient image of a locally compact space; the class of 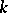 -spaces contains all Hausdorff spaces satisfying the first axiom of countability and all locally compact Hausdorff spaces.)
-spaces contains all Hausdorff spaces satisfying the first axiom of countability and all locally compact Hausdorff spaces.)
The topology of a metrizable uniform space is paracompact, by Stone's theorem. However, Isbell's problem on the uniform paracompactness of metrizable uniform spaces has been solved negatively. An example of a metrizable uniform space having a uniform covering with no locally finite uniform refinement has been constructed [3].
In the dimension theory of uniform spaces, the uniform dimension invariants 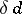 and
and 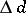 , defined by analogy with the topological dimension
, defined by analogy with the topological dimension 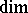 (
(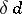 using finite uniform coverings and
using finite uniform coverings and 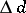 using all uniform coverings), and the uniform inductive dimension
using all uniform coverings), and the uniform inductive dimension 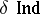 are basic. The dimension
are basic. The dimension 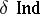 is defined by analogy with the large inductive dimension
is defined by analogy with the large inductive dimension 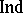 , by induction relative to the dimensions of proximity partitions between distant (in the sense of the proximity induced by the uniformity) sets. Here, a set
, by induction relative to the dimensions of proximity partitions between distant (in the sense of the proximity induced by the uniformity) sets. Here, a set  is called a proximity partition between
is called a proximity partition between 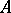 and
and 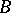 (where
(where 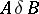 ) if for any
) if for any  -neighbourhood
-neighbourhood 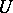 of
of 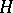 such that
such that  one has
one has 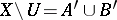 , where
, where  ,
,  ,
, 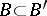 (
( is called a
is called a 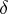 -neighbourhood of
-neighbourhood of 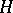 if
if 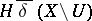 ). Thus, the dimension
). Thus, the dimension  (as well as
(as well as 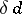 ) is not only a uniform but also a proximity invariant. The dimension
) is not only a uniform but also a proximity invariant. The dimension 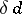 of a uniform space
of a uniform space 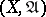 coincides with the ordinary dimension
coincides with the ordinary dimension 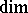 of the Samuel extension, constructed relative to the pre-compact uniformity equivalent to
of the Samuel extension, constructed relative to the pre-compact uniformity equivalent to 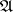 . If
. If 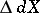 is finite, then
is finite, then  . However, it may happen that
. However, it may happen that 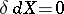 and
and 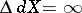 . For a metrizable uniform space
. For a metrizable uniform space 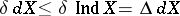 (and if
(and if 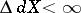 , then
, then 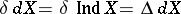 ). The equalities
). The equalities 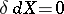 and
and 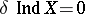 are equivalent for any uniform space. If a uniform space is metrizable, then the equalities
are equivalent for any uniform space. If a uniform space is metrizable, then the equalities 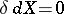 and
and  are also equivalent. If a uniform space
are also equivalent. If a uniform space 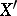 is an everywhere-dense subset of a uniform space
is an everywhere-dense subset of a uniform space 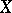 , then
, then 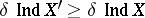 . Always:
. Always: 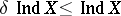 . For the dimension
. For the dimension 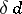 there is an analogue of the theorem on partitions.
there is an analogue of the theorem on partitions.
Various generalizations of uniform spaces have been obtained by weakening the axioms of a uniformity. Thus, in the axiomatics of a quasi-uniformity (see [8]) the symmetry axiom is excluded. For the definition of a generalized uniformity (see [10]) (an 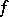 -uniformity), uniform families of subsets of
-uniformity), uniform families of subsets of 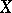 , which in general are not coverings, are used instead of uniform coverings (most of these families turn out to be everywhere-dense in the topology generated by the
, which in general are not coverings, are used instead of uniform coverings (most of these families turn out to be everywhere-dense in the topology generated by the 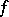 -uniformity). One of the generalizations of a uniformity — the so-called
-uniformity). One of the generalizations of a uniformity — the so-called 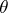 -uniformity — is connected with the presence of the topology on a uniform space. It is defined by families of
-uniformity — is connected with the presence of the topology on a uniform space. It is defined by families of 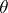 -coverings of a Hausdorff space; a
-coverings of a Hausdorff space; a 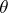 -covering is a system
-covering is a system 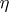 of canonical open sets of
of canonical open sets of 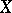 satisfying the following condition: For any
satisfying the following condition: For any 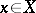 there are
there are 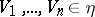 such that
such that 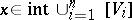 .
.
References
| [1] | A. Weil, "Sur les espaces à structure uniforme et sur la topologie générale" , Hermann (1938) |
| [2] | N. Bourbaki, "General topology" , Elements of mathematics , Springer (1989) (Translated from French) |
| [3] | E.V. Shchepin, "On a problem of Isbell" Soviet. Math. Dokl. , 16 : 3 (1975) pp. 685–687 Dokl. Akad. Nauk SSSR , 222 : 3 (1975) pp. 541–543 |
| [4] | J.W. Tukey, "Convergence and uniformity in topology" , Princeton Univ. Press (1940) |
| [5] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [6] | J.R. Isbell, "Uniform spaces" , Amer. Math. Soc. (1964) |
| [7] | P. Samuel, "Ultrafilters and compactification of uniform spaces" Trans. Amer. Math. Soc. , 64 (1948) pp. 100–132 |
| [8] | A. Császár, "Foundations of general topology" , Pergamon (1963) |
| [9] | V.V. Fedorchuk, "Uniform spaces and perfect irreducible mappings of topological spaces" Soviet Math. Dokl. , 11 : 3 (1970) pp. 818–820 Dokl. Akad. Nauk. SSSR , 192 : 6 (1970) pp. 1228–1230 |
| [10] | W. Kulpa, "A note on the dimension Dind" Colloq. Math. , 25 (1972) pp. 227–240 |
Comments
Pre-compact uniform spaces are also called totally bounded, and universal uniformities are also called fine uniformities.
Another description of  -spaces is as follows: A Hausdorff space
-spaces is as follows: A Hausdorff space 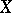 is a
is a 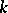 -space if and only if it satisfies the following condition: A subset of
-space if and only if it satisfies the following condition: A subset of 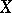 is closed in
is closed in 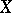 if and only if its intersection with every compact subset of
if and only if its intersection with every compact subset of 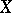 is closed.
is closed.
The construction of a metrizable uniform space that is not uniformly paracompact (i.e. has no base of (uniformly) locally finite uniform coverings) was done independently by E.V. Shchepin [3] and J. Pelant [a1]. In [a1] it is also shown that in some models of set theory (ZFC), the uniform coverings of a uniform space of power at most  need not form a base for a uniformity.
need not form a base for a uniformity.
References
| [a1] | J. Pelant, "Cardinal reflections and point-character of uniformities - counterexamples" , Sem. Uniform Spaces (Prague, 1973–1974) , Mat. Ustav. ČSAV, Prague (1975) pp. 149–158 |
| [a2] | R. Engelking, "General topology" , Heldermann (1989) |
Uniform space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_space&oldid=14627