Uniform continuity
A property of a function (mapping) 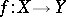 , where
, where 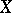 and
and 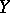 are metric spaces. It requires that for any
are metric spaces. It requires that for any 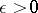 there is a
there is a 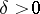 such that for all
such that for all 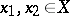 satisfying
satisfying 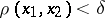 , the inequality
, the inequality 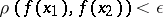 holds.
holds.
If a mapping 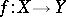 is continuous on
is continuous on 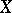 and
and 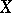 is a compactum, then
is a compactum, then 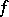 is uniformly continuous on
is uniformly continuous on 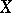 . The composite of uniformly-continuous mappings is uniformly continuous.
. The composite of uniformly-continuous mappings is uniformly continuous.
Uniform continuity of mappings occurs also in the theory of topological groups. For example, a mapping 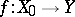 , where
, where 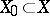 ,
, 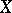 and
and 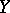 topological groups, is said to be uniformly continuous if for any neighbourhood of the identity
topological groups, is said to be uniformly continuous if for any neighbourhood of the identity  in
in 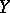 , there is a neighbourhood of the identity
, there is a neighbourhood of the identity 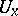 in
in 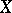 such that for any
such that for any 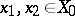 satisfying
satisfying 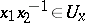 (respectively,
(respectively, 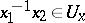 ), the inclusion
), the inclusion 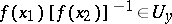 (respectively,
(respectively, 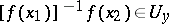 ) holds.
) holds.
The notion of uniform continuity has been generalized to mappings of uniform spaces (cf. Uniform space).
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [3] | J.L. Kelley, "General topology" , Springer (1975) |
| [4] | N. Bourbaki, "General topology" , Elements of mathematics , Springer (1989) (Translated from French) |
Comments
There are several natural uniform structures on a topological group; the (confusing) statement above about uniform continuity of mappings between them can be interpreted in various ways.
References
| [a1] | W. Roelcke, S. Dierolf, "Uniform structures on topological groups and their quotients" , McGraw-Hill (1981) |
| [a2] | R. Engelking, "General topology" , Heldermann (1989) |
Uniform continuity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_continuity&oldid=12797