Two-term congruence
binomial congruence, power congruence
An algebraic congruence of the form
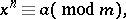 | (1) |
where  are coprime integers and
are coprime integers and  is a natural number. If the congruence (1) is solvable,
is a natural number. If the congruence (1) is solvable,  is called an
is called an  -th power residue modulo
-th power residue modulo 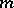 ; otherwise,
; otherwise,  is an
is an  -th power non-residue modulo
-th power non-residue modulo  .
.
The problem of solvability of a two-term congruence to a composite modulus 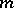 can be reduced to the study of the corresponding problem to a prime modulus
can be reduced to the study of the corresponding problem to a prime modulus  (cf. Congruence (in algebra)). For the prime modulus power congruence problem there is a solvability criterion, due to L. Euler: For the congruence
(cf. Congruence (in algebra)). For the prime modulus power congruence problem there is a solvability criterion, due to L. Euler: For the congruence
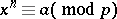 |
to be solvable, it is necessary that
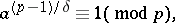 |
where 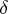 is the greatest common divisor of the numbers
is the greatest common divisor of the numbers  and
and  ; if this condition is met, the congruence in question has exactly
; if this condition is met, the congruence in question has exactly 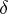 solutions.
solutions.
It follows immediately from Euler's criterion that the numbers 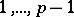 have exactly
have exactly 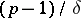
 -th power residues and
-th power residues and 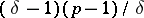 non-residues modulo
non-residues modulo 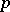 .
.
The converse problem is much more complicated: To find all moduli 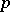 to which a given number
to which a given number  is a residue (or a non-residue) of power
is a residue (or a non-residue) of power 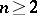 . It was established by Euler that the solvability or non-solvability of the congruence
. It was established by Euler that the solvability or non-solvability of the congruence  (
( ) depends on whether or not the prime modulus
) depends on whether or not the prime modulus 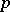 forms part of certain arithmetical progressions. A rigorous proof of this result was given first by C.F. Gauss in 1801 (see [4] and Gauss reciprocity law; Quadratic reciprocity law). Gauss further noted that a complete solution of the problem for
forms part of certain arithmetical progressions. A rigorous proof of this result was given first by C.F. Gauss in 1801 (see [4] and Gauss reciprocity law; Quadratic reciprocity law). Gauss further noted that a complete solution of the problem for 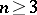 is only possible if the ring of rational integers is extended somewhat. Thus, in establishing the reciprocity law for biquadratic residues he was forced to extend the ring of rational integers to the ring of complex integers
is only possible if the ring of rational integers is extended somewhat. Thus, in establishing the reciprocity law for biquadratic residues he was forced to extend the ring of rational integers to the ring of complex integers  . The solvability or non-solvability of the biquadratic congruence
. The solvability or non-solvability of the biquadratic congruence  (
(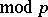 ) in the ring
) in the ring  for a given
for a given 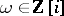 will depend on the value of the residue of the number
will depend on the value of the residue of the number 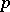 to some constant modulus
to some constant modulus  of the ring
of the ring 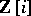 .
.
A new stage in the study of two-term congruences and their applications to other theoretical problems was initiated by I.M. Vinogradov, who showed in 1914 that the number 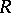 of quadratic residues to the prime modulus
of quadratic residues to the prime modulus 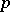 among the numbers
among the numbers 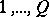 ,
, 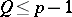 , is given by the formula
, is given by the formula
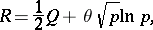 |
where 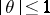 . A similar result was subsequently obtained by Vinogradov for a more general problem on the number of solutions of the congruence
. A similar result was subsequently obtained by Vinogradov for a more general problem on the number of solutions of the congruence
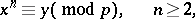 |
when  runs through an incomplete system of residues
runs through an incomplete system of residues  .
.
References
| [1] | B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [2] | I.M. [I.M. Vinogradov] Winogradow, "Elemente der Zahlentheorie" , R. Oldenbourg (1956) (Translated from Russian) |
| [3] | I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) |
| [4] | C.F. Gauss, "Untersuchungen über höhere Arithmetik" , A. Maser (1889) (Translated from Latin) |
Comments
In [a2] it is shown that the smallest non-quadratic residue modulo a prime 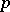 is smaller than
is smaller than  for any
for any  .
.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. 6 |
| [a2] | D.A. Burgess, "The distribution of quadratic residues and non-residues" Mathematica , 4 (1957) pp. 106–112 |
Two-term congruence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-term_congruence&oldid=12675