Two-constants theorem
Let  be a finitely-connected Jordan domain in the
be a finitely-connected Jordan domain in the  -plane and let
-plane and let  be a regular analytic function in
be a regular analytic function in  satisfying the inequality
satisfying the inequality  , as well as the relation
, as well as the relation
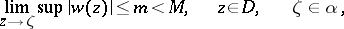 |
on some arc  of the boundary
of the boundary  . Then, at each point
. Then, at each point  of the set
of the set
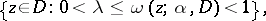 |
where  is the harmonic measure of the arc
is the harmonic measure of the arc  with respect to
with respect to 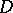 at
at  , the inequality
, the inequality
 |
is satisfied. If for some  (satisfying the condition
(satisfying the condition 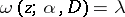 ) equality is attained, equality will hold for all
) equality is attained, equality will hold for all  and for all
and for all 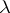 ,
, 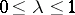 , while the function
, while the function 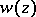 in this case has the form
in this case has the form
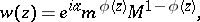 |
where  is a real number and
is a real number and 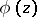 is an analytic function in
is an analytic function in  for which
for which  [1], [2].
[1], [2].
The two-constants theorem gives a quantitative expression of the unique determination of analytic functions by their boundary values and has important applications in the theory of functions [3]. Hadamard's three-circles theorem (cf. Hadamard theorem) is obtained from it as a special case. For possible analogues of the two-constants theorem for harmonic functions in space see [4], [5].
References
| [1] | F. Nevanlinna, R. Nevanlinna, "Über die Eigenschaften einer analytischen Funktion in der Umgebung einer singulären Stelle oder Linie" Acta Soc. Sci. Fennica , 5 : 5 (1922) |
| [2] | A. Ostrowski, "Über allgemeine Konvergenzsätze der komplexen Funktionentheorie" Jahresber. Deutsch. Math.-Ver. , 32 : 9–12 (1923) pp. 185–194 |
| [3] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [4] | S.N. Mergelyan, "Harmonic approximation and approximate solution of the Cauchy problem for the Laplace equation" Uspekhi Mat. Nauk , 11 : 5 (1956) pp. 3–26 (In Russian) |
| [5] | E.D. Solomentsev, "Three-spheres theorem for harmonic functions" Dokl. Akad. Nauk ArmSSR , 42 : 5 (1966) pp. 274–278 (In Russian) |
Comments
There is a more general  -constants theorem, [a2]: Let
-constants theorem, [a2]: Let  be holomorphic in a domain
be holomorphic in a domain  whose boundary is the union of
whose boundary is the union of  distinct rectifiable arcs
distinct rectifiable arcs  ; suppose that for each
; suppose that for each  there is a constant
there is a constant 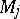 such that if
such that if  approaches any point of
approaches any point of 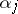 , then the limits of
, then the limits of 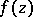 do not exceed
do not exceed  in absolute value. Then for each
in absolute value. Then for each 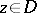 ,
,
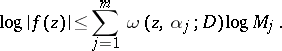 |
References
| [a1] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) pp. 210–214 (Translated from Russian) |
| [a2] | E. Hille, "Analytic function theory" , 2 , Chelsea, reprint (1987) pp. 409–410 |
Two-constants theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-constants_theorem&oldid=12855