Difference between revisions of "Tutte polynomial"
m (link) |
m (link) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 94 formulas, 91 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Let $M$ be a [[Matroid|matroid]] with rank function $r$ on the ground set $E$. The Tutte polynomial $t ( M ; x , y )$ of $M$ is defined by | ||
| − | + | \begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S )}. \end{equation*} | |
| − | + | One also writes $t ( M )$ for $t ( M ; x , y )$ when no confusion can arise about the values of $x$ and $y$. There are several equivalent reformulations of $t ( M )$; the most useful such expression is recursive, using the matroid operations of deletion and contraction: | |
| − | + | T0) If $E = \emptyset$, then $t ( M ) = 1$; | |
| − | + | T1) If $e$ is an isthmus, then $t ( M ) = x t ( M / e )$; | |
| + | |||
| + | T2) If $e$ is a loop, then $t ( M ) = y t ( M - e )$; | ||
| + | |||
| + | T3) If $e$ is neither an isthmus nor a loop, then $t ( M ) = t ( M / e ) + t ( M - e )$. | ||
Some standard evaluations of the Tutte polynomial are: | Some standard evaluations of the Tutte polynomial are: | ||
| − | a) | + | a) $t ( M ; 1,1 )$ is the number of bases of $M$; |
| − | b) | + | b) $t ( M ; 2,1 )$ is the number of independent subsets of $M$; |
| − | c) | + | c) $t ( M ; 1,2 )$ is the number of spanning subsets of $M$; |
| − | d) | + | d) $t ( M ; 2,2 ) = 2 ^ { | E | }$. |
| − | When a matroid | + | When a matroid $M$ is constructed from other matroids $M _ { 1 } , M _ { 2 } , \ldots$, it is frequently possible to compute $t ( M )$ from the $t ( M _ { i } )$. The most fundamental structural result of this kind concerns the direct sum of matroids: $t ( M _ { 1 } \oplus M _ { 2 } ) = t ( M _ { 1 } ) t ( M _ { 2 } )$. Another fundamental structural property of the Tutte polynomial is its transparent relationship with matroid duality: $t ( M ^ { * } ; x , y ) = t ( M ; y , x )$. Many related results can be found in [[#References|[a3]]]. |
| − | The Tutte polynomial has many significant connections with invariants in [[Graph theory|graph theory]]. Of central importance is the relationship between | + | The Tutte polynomial has many significant connections with invariants in [[Graph theory|graph theory]]. Of central importance is the relationship between $t ( M )$ and the [[chromatic polynomial]] $\chi ( G ; \lambda )$ of a graph $G$ (cf. also [[Graph colouring|Graph colouring]]). If $G$ is a graph having $v ( G )$ vertices and $c ( G )$ connected components, then |
| − | + | \begin{equation*} \chi ( G ; \lambda ) = \lambda ^ { c ( G ) } ( - 1 ) ^ { v ( G ) - c ( G ) } t ( M _ { G } , 1 - \lambda , 0 ), \end{equation*} | |
| − | where | + | where $M _ { G }$ is the cycle matroid of $G$ (cf. also [[Matroid|Matroid]]). Thus, when $G$ is planar (cf. [[Graph, planar|Graph, planar]]), $t ( M _ { G } ; x , y )$ simultaneously carries information concerning proper colourings of $G$ along with proper colourings of its [[dual graph]] $G ^ { * }$. This is the reason W.T. Tutte referred to it as a dichromatic polynomial in his foundational work in this area [[#References|[a14]]]. The polynomial was generalized from graphs to matroids by H.H. Crapo [[#References|[a5]]] and T.H. Brylawski [[#References|[a2]]]. |
| − | Other invariants which can be obtained from the Tutte polynomial include the beta invariant | + | Other invariants which can be obtained from the Tutte polynomial include the beta invariant $\beta ( M )$, the Möbius function $\mu ( M )$, and the characteristic polynomial $p ( M ; \lambda )$ of a matroid $M$. See [[#References|[a16]]] for more information about these invariants. |
==Applications== | ==Applications== | ||
The Tutte polynomial has applications in various areas, some of which are given below. For an extensive introduction, see [[#References|[a4]]]. | The Tutte polynomial has applications in various areas, some of which are given below. For an extensive introduction, see [[#References|[a4]]]. | ||
| − | [[Acyclic orientation]]s: Let | + | [[Acyclic orientation]]s: Let $a ( G )$ denote the number of acyclic orientations of a graph $G$. Then R. Stanley [[#References|[a13]]] proved that $a ( G ) = t ( M _ { G } ; 2,0 )$. A variety of related evaluations appear in [[#References|[a9]]]. |
| − | The critical problem of Crapo and G.-C. Rota [[#References|[a7]]]: Let | + | The critical problem of Crapo and G.-C. Rota [[#References|[a7]]]: Let $M$ be a rank-$r$ matroid which is represented over $\operatorname {GF} ( q )$ by $\phi : E \rightarrow \operatorname {GF} ( q ) ^ { n }$ and let $k$ be a positive integer. Then the number of $k$-tuples of linear functionals on $\operatorname{GF} ( q ) ^ { n }$ which distinguish $\phi ( E )$ equals $( - 1 ) ^ { r } q ^ { k ( n - r ) } t ( M ; 1 - q ^ { k } , 0 )$. See [[#References|[a12]]] for extensions of the critical problem. |
| − | Coding theory: Let | + | Coding theory: Let $C$ be a linear [[Code|code]] over $\operatorname {GF} ( q )$ with code-weight polynomial $A ( C ; q , z ) = \sum _ { \mathbf{v} \in C } z ^ { w (\mathbf{v}) }$, where $w ( \mathbf{v} )$ is the weight of the code word $\mathbf{v}$ (see also [[Coding and decoding|Coding and decoding]]). Then |
| − | + | \begin{equation*} A ( C , q , z ) = ( 1 - z ) ^ { r } z ^ { n - r } t \left( M _ { C } ; \frac { 1 + ( q - 1 ) z } { 1 - z } , \frac { 1 } { z } \right), \end{equation*} | |
| − | where | + | where $M _ { C }$ is the matroid associated with the code $C$. Many standard results in coding theory have interpretations using the Tutte polynomial [[#References|[a4]]]. |
| − | [[Arrangement of hyperplanes|Hyperplane arrangements]]: The number of regions in a central arrangement of hyperplanes is given by | + | [[Arrangement of hyperplanes|Hyperplane arrangements]]: The number of regions in a central arrangement of hyperplanes is given by $t ( M _ { H } ; 2,0 )$, where $M _ { H }$ is the matroid associated with the arrangement. Many generalizations of this result appear in [[#References|[a15]]]. |
| − | [[Combinatorial topology]]: The independent subsets of a matroid form a [[shellable | + | [[Combinatorial topology]]: The independent subsets of a matroid form a [[shellable complex]]. If $h _ { M } ( x )$ is the shelling polynomial associated with this complex, then $h _ { M } ( x ) = t ( x , 1 )$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120210/t12021074.png"/>. This result is analogous to the dichromatic interpretation for planar graphs. See [[#References|[a1]]] for more information on how the Tutte polynomial is associated to simplicial complexes. |
| − | [[Statistical mechanics, mathematical problems in|Statistical mechanics]], network reliability and [[knot theory]]: Suppose | + | [[Statistical mechanics, mathematical problems in|Statistical mechanics]], network reliability and [[knot theory]]: Suppose $M$ is a probabilistic matroid, i.e., each $e \in E$ has an independent probability $p ( e )$ of successful operation. The formula |
| − | + | \begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } \left( \prod _ { e \in S } p ( e ) \right) \left( \prod _ { e \notin S } ( 1 - p ( e ) ) \right)\times \end{equation*} | |
| − | + | \begin{equation*} \times ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( s )} \end{equation*} | |
| − | then produces a probabilistic Tutte polynomial. In this more general situation, | + | then produces a probabilistic Tutte polynomial. In this more general situation, $t ( M ; 1,2 )$ is the reliability of $M$, i.e., the probability that a randomly chosen subset spans $E$. Related Tutte polynomials have applications in statistical mechanics and network reliability [[#References|[a5]]] and knot theory [[#References|[a11]]]. |
| − | [[Greedoid]]s: When | + | [[Greedoid]]s: When $G$ is a greedoid (cf. also [[Greedy algorithm|Greedy algorithm]]), the expansion $t ( G ; x , y ) = \sum_{ S \subseteq E} ( x - 1 ) ^ { r ( G ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S ) }$ remains valid. The recursion of T3) takes a slightly different form, however: If $e$ is feasible, then $t ( G ) = t ( G / e ) + ( x - 1 ) ^ { r ( G ) - r ( G - e ) } t ( G - e )$. There are many combinatorial structures which admit a greedoid rank function in a natural way, but do not possess a meaningful matroid structure. For example, if $T _ { 1 }$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120210/t12021088.png"/> are [[rooted tree]]s (cf. also [[Tree]]), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120210/t12021091.png"/> are isomorphic as rooted trees [[#References|[a8]]]. |
| − | In general, it is | + | In general, it is $\cal N P$-hard (cf. [[NP|$\cal N P$]]) to compute the Tutte polynomial of a graph or a matroid [[#References|[a10]]]. Certain evaluations are computable in polynomial-time for certain classes of matroids, however. For example, the number of spanning trees of a graph can be calculated in polynomial-time by the matrix-tree theorem; since this number equals $t ( M ; 1,1 )$, this evaluation is tractable. |
====References==== | ====References==== | ||
<table> | <table> | ||
| − | < | + | <tr><td valign="top">[a1]</td> <td valign="top"> A. Björner, "The homology and shellability of matroids and geometric lattices" N. White (ed.) , ''Matroid Applications'' , ''Encycl. Math. Appl.'' , '''40''' , Cambridge Univ. Press (1992) pp. 226–283</td></tr> |
| − | < | + | <tr><td valign="top">[a2]</td> <td valign="top"> T.H. Brylawski, "The Tutte–Grothendieck ring" ''Algebra Univ.'' , '''2''' (1972) pp. 375–388</td></tr> |
| − | < | + | <tr><td valign="top">[a3]</td> <td valign="top"> T.H. Brylawski, "The Tutte polynomial. Part 1: General theory" A. Barlotti (ed.) , ''Matroid Theory and its Applications Proc. Third Mathematics Summer Center C.I.M.E.'' , Liguori, Naples (1980) pp. 125–275</td></tr> |
| − | < | + | <tr><td valign="top">[a4]</td> <td valign="top"> T.H. Brylawski, J.G. Oxley, "The Tutte polynomial and its applications" N. White (ed.) , ''Matroid Applications'' , ''Encycl. Math. Appl.'' , '''40''' , Cambridge Univ. Press (1992) pp. 123–225</td></tr> |
| − | < | + | <tr><td valign="top">[a5]</td> <td valign="top"> C.J. Colbourn, "The combinatorics of network reliability" , Oxford Univ. Press (1987)</td></tr> |
| − | < | + | <tr><td valign="top">[a6]</td> <td valign="top"> H.H. Crapo, "The Tutte polynomial" ''Aequat. Math.'' , '''3''' (1969) pp. 211–229</td></tr> |
| − | < | + | <tr><td valign="top">[a7]</td> <td valign="top"> H.H. Crapo, G.-C. Rota, "On the foundations of combinatorial theory: Combinatorial geometries" , MIT (1970) (Edition: Preliminary)</td></tr> |
| − | < | + | <tr><td valign="top">[a8]</td> <td valign="top"> G.P. Gordon, E.W. McMahon, "A greedoid polynomial which distinguishes rooted arborescences" ''Proc. Amer. Math. Soc.'' , '''107''' (1989) pp. 287–298</td></tr> |
| − | < | + | <tr><td valign="top">[a9]</td> <td valign="top"> C. Greene, T. Zaslavsky, "On the interpretation of Whitney numbers through arrangements of hyperplanes, zonotopes, non–Radon partitions, and orientations of graphs" ''Trans. Amer. Math. Soc.'' , '''280''' (1983) pp. 97–126</td></tr> |
| − | < | + | <tr><td valign="top">[a10]</td> <td valign="top"> F. Jaeger, D.L. Vertigan, D.J.A. Welsh, "On the computational complexity of the Jones and Tutte polynomials" ''Math. Proc. Cambridge Philos. Soc.'' , '''108''' (1990) pp. 35–53</td></tr> |
| − | < | + | <tr><td valign="top">[a11]</td> <td valign="top"> L. Kauffman, "Knots and physics" , World Sci. (1993) (Edition: Second)</td></tr> |
| − | < | + | <tr><td valign="top">[a12]</td> <td valign="top"> J.P.S. Kung, "Critical problems" J. Bonin (ed.) et al. (ed.) , ''Matroid Theory'' , ''Contemp. Math.'' , '''197''' , Amer. Math. Soc. (1996) pp. 1–128</td></tr> |
| − | < | + | <tr><td valign="top">[a13]</td> <td valign="top"> R.P. Stanley, "Acyclic orientations of graphs" ''Discrete Math.'' , '''5''' (1973) pp. 171–178</td></tr> |
| − | < | + | <tr><td valign="top">[a14]</td> <td valign="top"> W.T. Tutte, "A contribution to the theory of chromatic polynomials" ''Canad. J. Math.'' , '''6''' (1954) pp. 80–91</td></tr> |
| − | < | + | <tr><td valign="top">[a15]</td> <td valign="top"> T. Zaslavsky, "Facing up to arrangements: Face-count formulas for partitions of space by hyperplanes" ''Memoirs Amer. Math. Soc.'' , '''154''' (1975)</td></tr> |
| − | < | + | <tr><td valign="top">[a16]</td> <td valign="top"> T. Zaslavsky, "The Möbius functions and the characteristic polynomial" N. White (ed.) , ''Combinatorial Geometries'' , ''Encycl. Math. Appl.'' , '''29''' , Cambridge Univ. Press (1987) pp. 114–138</td></tr> |
</table> | </table> | ||
Revision as of 11:16, 30 June 2021
Let $M$ be a matroid with rank function $r$ on the ground set $E$. The Tutte polynomial $t ( M ; x , y )$ of $M$ is defined by
\begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S )}. \end{equation*}
One also writes $t ( M )$ for $t ( M ; x , y )$ when no confusion can arise about the values of $x$ and $y$. There are several equivalent reformulations of $t ( M )$; the most useful such expression is recursive, using the matroid operations of deletion and contraction:
T0) If $E = \emptyset$, then $t ( M ) = 1$;
T1) If $e$ is an isthmus, then $t ( M ) = x t ( M / e )$;
T2) If $e$ is a loop, then $t ( M ) = y t ( M - e )$;
T3) If $e$ is neither an isthmus nor a loop, then $t ( M ) = t ( M / e ) + t ( M - e )$.
Some standard evaluations of the Tutte polynomial are:
a) $t ( M ; 1,1 )$ is the number of bases of $M$;
b) $t ( M ; 2,1 )$ is the number of independent subsets of $M$;
c) $t ( M ; 1,2 )$ is the number of spanning subsets of $M$;
d) $t ( M ; 2,2 ) = 2 ^ { | E | }$.
When a matroid $M$ is constructed from other matroids $M _ { 1 } , M _ { 2 } , \ldots$, it is frequently possible to compute $t ( M )$ from the $t ( M _ { i } )$. The most fundamental structural result of this kind concerns the direct sum of matroids: $t ( M _ { 1 } \oplus M _ { 2 } ) = t ( M _ { 1 } ) t ( M _ { 2 } )$. Another fundamental structural property of the Tutte polynomial is its transparent relationship with matroid duality: $t ( M ^ { * } ; x , y ) = t ( M ; y , x )$. Many related results can be found in [a3].
The Tutte polynomial has many significant connections with invariants in graph theory. Of central importance is the relationship between $t ( M )$ and the chromatic polynomial $\chi ( G ; \lambda )$ of a graph $G$ (cf. also Graph colouring). If $G$ is a graph having $v ( G )$ vertices and $c ( G )$ connected components, then
\begin{equation*} \chi ( G ; \lambda ) = \lambda ^ { c ( G ) } ( - 1 ) ^ { v ( G ) - c ( G ) } t ( M _ { G } , 1 - \lambda , 0 ), \end{equation*}
where $M _ { G }$ is the cycle matroid of $G$ (cf. also Matroid). Thus, when $G$ is planar (cf. Graph, planar), $t ( M _ { G } ; x , y )$ simultaneously carries information concerning proper colourings of $G$ along with proper colourings of its dual graph $G ^ { * }$. This is the reason W.T. Tutte referred to it as a dichromatic polynomial in his foundational work in this area [a14]. The polynomial was generalized from graphs to matroids by H.H. Crapo [a5] and T.H. Brylawski [a2].
Other invariants which can be obtained from the Tutte polynomial include the beta invariant $\beta ( M )$, the Möbius function $\mu ( M )$, and the characteristic polynomial $p ( M ; \lambda )$ of a matroid $M$. See [a16] for more information about these invariants.
Applications
The Tutte polynomial has applications in various areas, some of which are given below. For an extensive introduction, see [a4].
Acyclic orientations: Let $a ( G )$ denote the number of acyclic orientations of a graph $G$. Then R. Stanley [a13] proved that $a ( G ) = t ( M _ { G } ; 2,0 )$. A variety of related evaluations appear in [a9].
The critical problem of Crapo and G.-C. Rota [a7]: Let $M$ be a rank-$r$ matroid which is represented over $\operatorname {GF} ( q )$ by $\phi : E \rightarrow \operatorname {GF} ( q ) ^ { n }$ and let $k$ be a positive integer. Then the number of $k$-tuples of linear functionals on $\operatorname{GF} ( q ) ^ { n }$ which distinguish $\phi ( E )$ equals $( - 1 ) ^ { r } q ^ { k ( n - r ) } t ( M ; 1 - q ^ { k } , 0 )$. See [a12] for extensions of the critical problem.
Coding theory: Let $C$ be a linear code over $\operatorname {GF} ( q )$ with code-weight polynomial $A ( C ; q , z ) = \sum _ { \mathbf{v} \in C } z ^ { w (\mathbf{v}) }$, where $w ( \mathbf{v} )$ is the weight of the code word $\mathbf{v}$ (see also Coding and decoding). Then
\begin{equation*} A ( C , q , z ) = ( 1 - z ) ^ { r } z ^ { n - r } t \left( M _ { C } ; \frac { 1 + ( q - 1 ) z } { 1 - z } , \frac { 1 } { z } \right), \end{equation*}
where $M _ { C }$ is the matroid associated with the code $C$. Many standard results in coding theory have interpretations using the Tutte polynomial [a4].
Hyperplane arrangements: The number of regions in a central arrangement of hyperplanes is given by $t ( M _ { H } ; 2,0 )$, where $M _ { H }$ is the matroid associated with the arrangement. Many generalizations of this result appear in [a15].
Combinatorial topology: The independent subsets of a matroid form a shellable complex. If $h _ { M } ( x )$ is the shelling polynomial associated with this complex, then $h _ { M } ( x ) = t ( x , 1 )$ and 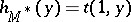 . This result is analogous to the dichromatic interpretation for planar graphs. See [a1] for more information on how the Tutte polynomial is associated to simplicial complexes.
. This result is analogous to the dichromatic interpretation for planar graphs. See [a1] for more information on how the Tutte polynomial is associated to simplicial complexes.
Statistical mechanics, network reliability and knot theory: Suppose $M$ is a probabilistic matroid, i.e., each $e \in E$ has an independent probability $p ( e )$ of successful operation. The formula
\begin{equation*} t ( M ; x , y ) = \sum _ { S \subseteq E } \left( \prod _ { e \in S } p ( e ) \right) \left( \prod _ { e \notin S } ( 1 - p ( e ) ) \right)\times \end{equation*}
\begin{equation*} \times ( x - 1 ) ^ { r ( M ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( s )} \end{equation*}
then produces a probabilistic Tutte polynomial. In this more general situation, $t ( M ; 1,2 )$ is the reliability of $M$, i.e., the probability that a randomly chosen subset spans $E$. Related Tutte polynomials have applications in statistical mechanics and network reliability [a5] and knot theory [a11].
Greedoids: When $G$ is a greedoid (cf. also Greedy algorithm), the expansion $t ( G ; x , y ) = \sum_{ S \subseteq E} ( x - 1 ) ^ { r ( G ) - r ( S ) } ( y - 1 ) ^ { | S | - r ( S ) }$ remains valid. The recursion of T3) takes a slightly different form, however: If $e$ is feasible, then $t ( G ) = t ( G / e ) + ( x - 1 ) ^ { r ( G ) - r ( G - e ) } t ( G - e )$. There are many combinatorial structures which admit a greedoid rank function in a natural way, but do not possess a meaningful matroid structure. For example, if $T _ { 1 }$ and 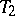 are rooted trees (cf. also Tree), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and
are rooted trees (cf. also Tree), then computing the Tutte polynomial in this way gives $t ( T _ { 1 } ) = t ( T _ { 2 } )$ if and only if $T _ { 1 }$ and 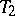 are isomorphic as rooted trees [a8].
are isomorphic as rooted trees [a8].
In general, it is $\cal N P$-hard (cf. $\cal N P$) to compute the Tutte polynomial of a graph or a matroid [a10]. Certain evaluations are computable in polynomial-time for certain classes of matroids, however. For example, the number of spanning trees of a graph can be calculated in polynomial-time by the matrix-tree theorem; since this number equals $t ( M ; 1,1 )$, this evaluation is tractable.
References
| [a1] | A. Björner, "The homology and shellability of matroids and geometric lattices" N. White (ed.) , Matroid Applications , Encycl. Math. Appl. , 40 , Cambridge Univ. Press (1992) pp. 226–283 |
| [a2] | T.H. Brylawski, "The Tutte–Grothendieck ring" Algebra Univ. , 2 (1972) pp. 375–388 |
| [a3] | T.H. Brylawski, "The Tutte polynomial. Part 1: General theory" A. Barlotti (ed.) , Matroid Theory and its Applications Proc. Third Mathematics Summer Center C.I.M.E. , Liguori, Naples (1980) pp. 125–275 |
| [a4] | T.H. Brylawski, J.G. Oxley, "The Tutte polynomial and its applications" N. White (ed.) , Matroid Applications , Encycl. Math. Appl. , 40 , Cambridge Univ. Press (1992) pp. 123–225 |
| [a5] | C.J. Colbourn, "The combinatorics of network reliability" , Oxford Univ. Press (1987) |
| [a6] | H.H. Crapo, "The Tutte polynomial" Aequat. Math. , 3 (1969) pp. 211–229 |
| [a7] | H.H. Crapo, G.-C. Rota, "On the foundations of combinatorial theory: Combinatorial geometries" , MIT (1970) (Edition: Preliminary) |
| [a8] | G.P. Gordon, E.W. McMahon, "A greedoid polynomial which distinguishes rooted arborescences" Proc. Amer. Math. Soc. , 107 (1989) pp. 287–298 |
| [a9] | C. Greene, T. Zaslavsky, "On the interpretation of Whitney numbers through arrangements of hyperplanes, zonotopes, non–Radon partitions, and orientations of graphs" Trans. Amer. Math. Soc. , 280 (1983) pp. 97–126 |
| [a10] | F. Jaeger, D.L. Vertigan, D.J.A. Welsh, "On the computational complexity of the Jones and Tutte polynomials" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 35–53 |
| [a11] | L. Kauffman, "Knots and physics" , World Sci. (1993) (Edition: Second) |
| [a12] | J.P.S. Kung, "Critical problems" J. Bonin (ed.) et al. (ed.) , Matroid Theory , Contemp. Math. , 197 , Amer. Math. Soc. (1996) pp. 1–128 |
| [a13] | R.P. Stanley, "Acyclic orientations of graphs" Discrete Math. , 5 (1973) pp. 171–178 |
| [a14] | W.T. Tutte, "A contribution to the theory of chromatic polynomials" Canad. J. Math. , 6 (1954) pp. 80–91 |
| [a15] | T. Zaslavsky, "Facing up to arrangements: Face-count formulas for partitions of space by hyperplanes" Memoirs Amer. Math. Soc. , 154 (1975) |
| [a16] | T. Zaslavsky, "The Möbius functions and the characteristic polynomial" N. White (ed.) , Combinatorial Geometries , Encycl. Math. Appl. , 29 , Cambridge Univ. Press (1987) pp. 114–138 |
Tutte polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tutte_polynomial&oldid=42759