Turbulence, mathematical problems in
The derivation, analysis and solution of equations describing turbulent flows of fluids and gases (that is, turbulent flows whose thermodynamic and hydrodynamic characteristics undergo chaotic fluctuations as a result of the presence of numerous eddies of varying sizes and therefore change in space and time in a very irregular fashion).
The individual realizations of turbulent flows are described by the ordinary equations of the hydrodynamics of a viscous fluid. The uniqueness of the solution of the Cauchy problem for them has not been proved (proofs have only been found for two-dimensional flows and under special assumptions concerning the variability of the kinematic viscosity  ). Stationary solutions corresponding to laminar flows exist formally for any Reynolds number
). Stationary solutions corresponding to laminar flows exist formally for any Reynolds number 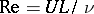 (where
(where 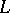 and
and 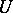 are the length and velocity scales), but for
are the length and velocity scales), but for 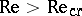 they are unstable. Hydrodynamic instability with respect to small perturbations of the velocity field of the form
they are unstable. Hydrodynamic instability with respect to small perturbations of the velocity field of the form
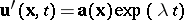 |
is studied as an eigenvalue problem of the corresponding linearized equation for 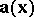 (the so-called Orr–Sommerfeld equation).
(the so-called Orr–Sommerfeld equation).
For values of the Reynolds number 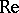 in some neighbourhood of
in some neighbourhood of 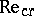 , in the phase space of the flow there exists a one-parameter family of closed trajectories. If this happens only for
, in the phase space of the flow there exists a one-parameter family of closed trajectories. If this happens only for  , then the bifurcation is called normal and the closed trajectories are limit cycles to which correspond periodic solutions in
, then the bifurcation is called normal and the closed trajectories are limit cycles to which correspond periodic solutions in 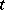 with finite amplitudes of order
with finite amplitudes of order 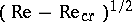 and arbitrary phases. According to a hypothesis of L.D. Landau (1944), turbulence is formed as a result of a sequence of normal bifurcations and is a quasi-periodic ergodic flow with a very large number of incommensurable oscillation frequencies and corresponding degrees of freedom, that is, phase oscillations.
and arbitrary phases. According to a hypothesis of L.D. Landau (1944), turbulence is formed as a result of a sequence of normal bifurcations and is a quasi-periodic ergodic flow with a very large number of incommensurable oscillation frequencies and corresponding degrees of freedom, that is, phase oscillations.
If the family of closed phase trajectories occurs even for 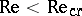 , then the bifurcation is called inverse, and the limit cycles are unstable (that is, the trajectories wind away from them); as
, then the bifurcation is called inverse, and the limit cycles are unstable (that is, the trajectories wind away from them); as 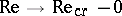 , they shrink and disappear, in the limit, while when
, they shrink and disappear, in the limit, while when 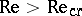 the perturbations increase with time and, apparently, rapidly acquire an aperiodic character. It is possible that in this case there is a strange attractor in the phase space, that is, a set
the perturbations increase with time and, apparently, rapidly acquire an aperiodic character. It is possible that in this case there is a strange attractor in the phase space, that is, a set 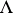 of non-wandering points (each neighbourhood of which is intersected by some trajectory at least twice), differing from the fixed points and closed trajectories, and having neighbourhoods in which all trajectories occurring there approach
of non-wandering points (each neighbourhood of which is intersected by some trajectory at least twice), differing from the fixed points and closed trajectories, and having neighbourhoods in which all trajectories occurring there approach 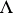 asymptotically.
asymptotically.
There is a conjecture that after four bifurcations in the phase space of the flow there appears a strange attractor which is locally a Cantor set of two-dimensional surfaces, and which when reached gives rise to the chaos of the flow, that is, turbulence. However, a bifurcation theory for hydrodynamical systems has not yet been constructed (see [3]).
The most complete statistical description of a turbulent flow of an incompressible fluid is a probability measure 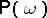 on the function space of possible velocity fields
on the function space of possible velocity fields 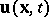 or its functional Fourier transform, called the characteristic functional (for example, in the spectral representation
or its functional Fourier transform, called the characteristic functional (for example, in the spectral representation 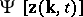 , see [1]). For this functional, a linear equation in variational derivatives is derived from the Navier–Stokes equations (so that the statistical dynamics of the turbulence turns out to be linear), which has to be solved for a given
, see [1]). For this functional, a linear equation in variational derivatives is derived from the Navier–Stokes equations (so that the statistical dynamics of the turbulence turns out to be linear), which has to be solved for a given
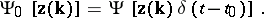 |
In particular, for the spatial characteristic functional 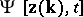 , describing the complete statistics of the velocity field at a fixed moment of time, one obtains the Hopf equation:
, describing the complete statistics of the velocity field at a fixed moment of time, one obtains the Hopf equation:
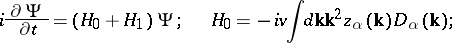 |
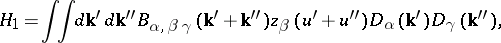 |
where
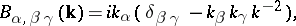 |
and 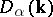 is the operator of variational differentiation with respect to
is the operator of variational differentiation with respect to 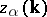 . This equation is analogous to the equation for the state
. This equation is analogous to the equation for the state 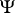 in the Schrödinger representation of the quantized Bose field with strong interaction of special type (the fusion of two bosons into one):
in the Schrödinger representation of the quantized Bose field with strong interaction of special type (the fusion of two bosons into one): 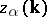 and
and 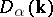 are the creation and annihilation operators of quanta with momentum
are the creation and annihilation operators of quanta with momentum 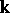 , while the Reynolds number
, while the Reynolds number 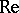 serves as the interaction constant. General methods for solving the linear equations in variational derivatives have yet to be created. When
serves as the interaction constant. General methods for solving the linear equations in variational derivatives have yet to be created. When 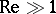 , perturbation theory does not work, although a partial summation of the Feynman diagrams is possible (see [2]). The solution
, perturbation theory does not work, although a partial summation of the Feynman diagrams is possible (see [2]). The solution 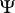 can be written in the form of a functional integral, but general methods for calculating such integrals do not yet exist. Nevertheless, a general method for finding the probability measure
can be written in the form of a functional integral, but general methods for calculating such integrals do not yet exist. Nevertheless, a general method for finding the probability measure 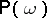 for the description of turbulent flows may be provided by the construction of such measures
for the description of turbulent flows may be provided by the construction of such measures 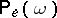 for Galerkin approximations of the Navier–Stokes equations: weak compactness has been proved for the family of measures
for Galerkin approximations of the Navier–Stokes equations: weak compactness has been proved for the family of measures 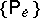 (see [6]); in particular, several uniqueness and existence theorems for the solutions
(see [6]); in particular, several uniqueness and existence theorems for the solutions 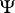 have been proved by this method.
have been proved by this method.
An equivalent formulation of the complete statistical description of a turbulent flow consists in specifying all finite-dimensional probability densities 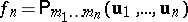 for the values
for the values 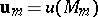 of the velocity field on all possible finite sets of points
of the velocity field on all possible finite sets of points 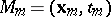 of space-time. For these one deduces from the Navier–Stokes equations (see [5]) the linear equations
of space-time. For these one deduces from the Navier–Stokes equations (see [5]) the linear equations
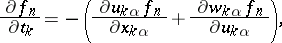 |
where 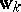 is the conditional mathematical expectation of the acceleration at the point
is the conditional mathematical expectation of the acceleration at the point 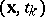 transferred to the point
transferred to the point 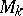 under the condition that the values
under the condition that the values 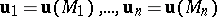 are fixed. The quantities
are fixed. The quantities 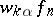 contain integrals of
contain integrals of 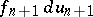 ; thus the equations for
; thus the equations for  form an infinite chain (similar to the Bogolyubov chain of equations). By integrating the equation for
form an infinite chain (similar to the Bogolyubov chain of equations). By integrating the equation for 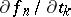 with respect to
with respect to 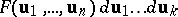 , one obtains the generalized Freedman–Keller equations
, one obtains the generalized Freedman–Keller equations
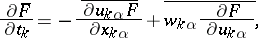 |
where the bar denotes mathematical expectation. This equation was derived for 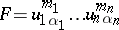 , so that
, so that 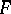 is the
is the  -point statistical moment of the velocity field of order
-point statistical moment of the velocity field of order 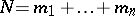 . The equations for the moments form an infinite chain (the solvability of which can be proved by means of Galerkin approximation of the Navier–Stokes equations).
. The equations for the moments form an infinite chain (the solvability of which can be proved by means of Galerkin approximation of the Navier–Stokes equations).
When 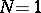 , these equations (the Reynolds equations) are obtained by direct averaging of the Navier–Stokes equations and differ from such equations for the averaged velocity field
, these equations (the Reynolds equations) are obtained by direct averaging of the Navier–Stokes equations and differ from such equations for the averaged velocity field 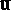 by the appearance of extra unknowns, namely, the one-point second moments
by the appearance of extra unknowns, namely, the one-point second moments 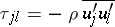 (where
(where  is the density of the fluid and the primes denote deviations from the mathematical expectations), called the Reynolds stresses. The simplest method for closing the Freedman–Keller system of equations is to represent the
is the density of the fluid and the primes denote deviations from the mathematical expectations), called the Reynolds stresses. The simplest method for closing the Freedman–Keller system of equations is to represent the 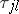 in the form of functions of
in the form of functions of 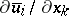 . In the so-called semi-empirical theory of turbulence these functions are taken to be linear, and their coefficients (having the meaning of coefficients of turbulent viscosity) are subjected to additional assumptions (for example, proportionality to
. In the so-called semi-empirical theory of turbulence these functions are taken to be linear, and their coefficients (having the meaning of coefficients of turbulent viscosity) are subjected to additional assumptions (for example, proportionality to 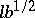 , where
, where 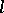 and
and 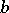 are the scale and kinetic energy of the turbulence per unit mass, for which supplementary equations are constructed; this makes the description of the averaged flow non-linear and creates special effects).
are the scale and kinetic energy of the turbulence per unit mass, for which supplementary equations are constructed; this makes the description of the averaged flow non-linear and creates special effects).
When 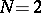 , one obtains equations for two-point correlation functions of the velocity field
, one obtains equations for two-point correlation functions of the velocity field 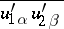 (or their Fourier transforms with respect to the
(or their Fourier transforms with respect to the 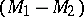 -spectral functions). For their closure, additional assumptions are necessary concerning the third moments that occur (see [1], [5]). The most natural methods for constructing closed equations for the spectra of the turbulence are obtained by cutting partially-summed Feynman diagrams.
-spectral functions). For their closure, additional assumptions are necessary concerning the third moments that occur (see [1], [5]). The most natural methods for constructing closed equations for the spectra of the turbulence are obtained by cutting partially-summed Feynman diagrams.
Substantial geometric simplifications are obtained in the case of homogeneous and isotropic turbulence. This model is important because every real turbulence with a large Reynolds number turns out to be locally stationary, locally homogeneous and locally isotropic. Furthermore, for fixed rate of dissipation of kinetic energy  , the statistical structure of a three-dimensional turbulent flow with a very large Reynolds number in sufficiently small scales is completely determined by the two parameters
, the statistical structure of a three-dimensional turbulent flow with a very large Reynolds number in sufficiently small scales is completely determined by the two parameters  and
and  , so that, for example, the structure velocity function for
, so that, for example, the structure velocity function for 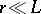 must have the form
must have the form
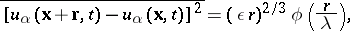 |
where 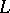 is the scale of the flow in the large and
is the scale of the flow in the large and 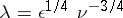 is the Kolmogorov internal scale; in the so-called inertial range
is the Kolmogorov internal scale; in the so-called inertial range 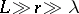 , the parameter
, the parameter  is suppressed and the function
is suppressed and the function 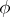 becomes a constant. On the other hand, if one takes into account the fluctuations of the field
becomes a constant. On the other hand, if one takes into account the fluctuations of the field  , then the Kolmogorov similarity becomes incomplete and the structure function acquires a correction factor
, then the Kolmogorov similarity becomes incomplete and the structure function acquires a correction factor 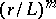 with a small exponent
with a small exponent 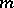 .
.
In two-dimensional flows, apart from the energy, the mean square of the vorticity, that is, the enstrophy, is still an adiabatic integral of the motion (so that the vorticity filaments do not stretch) and, in addition to the parameters  and
and  , there appears the rate of degeneration of the enstrophy,
, there appears the rate of degeneration of the enstrophy, 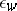 . Here one passes from the scales of energy-filled eddies to the large-scale region according to the Kolmogorov law, while the enstrophy passes to the small-scale region according to the non-local spectral law (see [4]):
. Here one passes from the scales of energy-filled eddies to the large-scale region according to the Kolmogorov law, while the enstrophy passes to the small-scale region according to the non-local spectral law (see [4]):
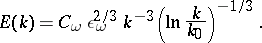 |
Such properties are possessed by large-scale quasi-two-dimensional turbulence in the atmosphere and in the ocean formed by synoptic eddies and Rossby waves. The role of the vorticity of a two-dimensional flow is played here by the so-called potential vorticity, which is the scalar product of the vorticity of the absolute velocity and the gradient of the entropy. The equation for this in the quasi-geostrophic approximation is obtained in the form
 |
where  ,
, 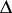 ,
, 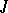 are the horizontal stream function, the Laplacian and the Jacobian,
are the horizontal stream function, the Laplacian and the Jacobian,  is the vertical coordinate,
is the vertical coordinate, 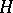 and
and 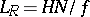 are the thickness of the layer and the Rossby "deformation radius" , respectively (
are the thickness of the layer and the Rossby "deformation radius" , respectively (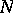 is the Waissala–Brent frequency,
is the Waissala–Brent frequency,  is the Coriolis parameter),
is the Coriolis parameter),  is an arc of a latitude circle,
is an arc of a latitude circle, 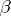 is the derivative of
is the derivative of 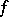 along the meridian, and
along the meridian, and 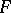 describes non-adiabatic factors. In the region
describes non-adiabatic factors. In the region 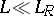 , the ordinary equation of two-dimensional turbulence is obtained. The wave number
, the ordinary equation of two-dimensional turbulence is obtained. The wave number 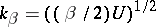 (where
(where  is the typical velocity) separates the eddies
is the typical velocity) separates the eddies 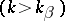 and the Rossby waves
and the Rossby waves 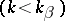 . Small initial eddies have the tendency to straighten along verticals with increasing time ( "barotropization" ), displaced towards the West and extending along latitude circles.
. Small initial eddies have the tendency to straighten along verticals with increasing time ( "barotropization" ), displaced towards the West and extending along latitude circles.
Important generalizations of turbulence in an incompressible fluid are turbulence in a stratified fluid with buoyancy forces, and magneto-hydrodynamic turbulence.
References
| [1] | A.S. Monin, A.M. Yaglom, "Fluid mechanics" , 1–2 , M.I.T. (1971–1975) (Translated from Russian) |
| [2] | E.B. Gledzer, A.S. Monin, "The method of diagrams in perturbation theory" Russian Math. Surveys , 29 : 3 (1974) pp. 117–168 Uspekhi Mat. Nauk , 29 : 3 (1974) pp. 111–159 |
| [3] | A.S. Monin, "On the nature of turbulence" Soviet Phys. Uspekhi , 21 : 5 (1978) pp. 429–442 Uspekhi Fiz. Nauk , 125 : 1 (1978) pp. 97–122 |
| [4] | A.P. Mirabel', A.S. Monin, Uspekhi Mekh. , 2 : 3 (1979) pp. 47–95 |
| [5] | A.S. Monin, R.V. Ozmidov, "Turbulence in the ocean" , Reidel (1985) (Translated from Russian) |
| [6] | M.I. Vishik, A.V. Fursikov, "Mathematical problems of statistical hydromechanics" , Kluwer (1988) (Translated from Russian) |
Comments
In 1983 O. Reynolds studied experimentally the flow of a fluid in a pipe with circular cross-section and found a transition from stationary laminar flow to irregular flow which was later named turbulent. However, all subsequent computations by linear stability analysis show that the basic laminar flow is stable to infinitesimal perturbations. Hence it is not true that for any laminar flow there is a critical 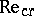 above which the flow is unstable. In fact, the fundamental Reynold experiment still baffles all attempts at a bifurcation analysis.
above which the flow is unstable. In fact, the fundamental Reynold experiment still baffles all attempts at a bifurcation analysis.
The Orr–Sommerfeld equation is not a universal equation for linear hydrodynamic stability analysis. It applies only to the so-called shear flows (see, for example, [a10]).
Landau's conjecture on the transition to turbulence is of historical interest, but has now (1991) generally been abandoned.
A standard reference on homogeneous turbulence is still [a11].
In the last decades the following main themes have evolved. In the statistical approach there are contributions along the lines set out by A.N. Kolmogorov, see [a1], [a2]. Assuming that the kinetic energy, 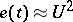 , decreases at a constant rate,
, decreases at a constant rate, 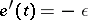 , one has the Kolmogorov relation
, one has the Kolmogorov relation 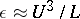 , where
, where 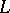 and
and 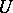 are the length and velocity scales of an eddy. The time scale of decay of an eddy equals
are the length and velocity scales of an eddy. The time scale of decay of an eddy equals 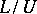 .
.
The effect of the non-linearity in the Navier–Stokes equation on the wave form of a free boundary is studied from approximating equations such as the Boussinesq equation and Burgers equation, the last one being of the form
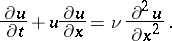 |
This equation has an exact solution. The onset of wirling patterns can be understood from the Kelvin–Helmholtz problem: At a free boundary with shear flow the linear waves are shown to be unstable. A non-linear analysis of instabilities (Eckhaus instability) has been performed with a non-linear modulation equation as starting point. For a theory of this so-called Ginzburg–Landau equation see [a3].
The idea that turbulence is due to the presence of a strange attractor in the dynamics of the flow has been expressed the first time in [a4], see also [a5] for an introductory exposition of this topic. In [a6] methods for estimating the fractal dimension of the attractor are given.
References
| [a1] | H. Tennekes, J.L. Lumley, "A first course in turbulence" , M.I.T. (1972) |
| [a2] | J.O. Hinze, "Turbulence" , McGraw-Hill (1975) |
| [a3] | G. Iooss, Y. Mielke, Y. Denay, "Theory of steady Ginzburg–Landau equation in hydrodynamic stability problems" Eur. J. Mech. B./Fluids , 8 (1989) pp. 229–268 |
| [a4] | D. Ruelle, F. Takens, "On the nature of turbulence" Comm. Math. Phys. , 20 (1971) pp. 167–192 |
| [a5] | P. Bergé, Y. Pomeau, C. Vidal, "Order within chaos" , Wiley (1984) |
| [a6] | P. Constantin, C. Foias, "Navier–Stokes equations" , Univ. Chicago Press (1988) |
| [a7] | M. Lesieur, "Turbulence in fluids" , Kluwer (1990) |
| [a8] | B.E. Lander, D.B. Spalding, "Mathematical models of turbulence" , Acad. Press (1972) |
| [a9] | M.T. Landahl, E. Mollo-Christensen, "Turbulence" , Cambridge Univ. Press (1986) |
| [a10] | C.C. Lin, "The theory of hydrodynamic stability" , Cambridge Univ. Press (1955) |
| [a11] | G.K. Batchelor, "The theory of homogeneous turbulence" , Cambridge Univ. Press (1956) |
Turbulence, mathematical problems in. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Turbulence,_mathematical_problems_in&oldid=17104