Turán theory
P. Turán introduced [a52] and developed (see [a9], [a10], [a11], [a12], [a13], [a14], [a16], [a21], [a22], [a23], [a24], [a25], [a26], [a27], [a28], [a29], [a30], [a31], [a32], [a33], [a34], [a35], [a36], [a37], [a38], [a39], [a40], [a41], [a46], and all papers by Turán mentioned below) the power sum method, by which one can investigate certain minimax problems described below. The method is used in many problems of analytic number theory, analysis and applied mathematics.
Let 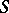 be a fixed set of integers. Let
be a fixed set of integers. Let 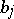 be fixed complex numbers and let
be fixed complex numbers and let 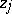 be complex numbers from a prescribed set. Define the following norms:
be complex numbers from a prescribed set. Define the following norms:
Bohr norm: 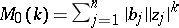 ;
;
minimum norm: 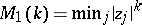 ;
;
maximum norm: 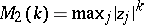 ;
;
Wiener norm: 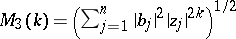 ;
;
separation norm: 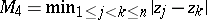 ;
;
Cauchy norm:  ;
;
argument norm: 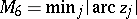 . Turán's method deals with the following problems [a91].
. Turán's method deals with the following problems [a91].
1) Determine, for 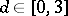 ,
,
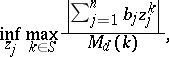 | (a1) |
where the infimum is taken over all complex numbers 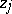 (two-sided direct problems).
(two-sided direct problems).
2) Find the above minimum in (a1) over all complex numbers 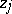 satisfying
satisfying 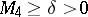 or
or 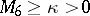 ( "two-sided conditional problems" ).
( "two-sided conditional problems" ).
3) For a given domain 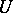 and
and 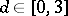 , find
, find
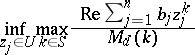 |
(one-sided conditional problems).
4) For a given weight function 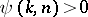 and
and 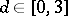 , find
, find
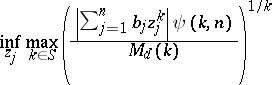 |
(weighted two-sided problems).
5) For a given domain  and
and  , find
, find
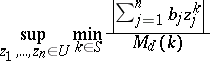 |
(dual conditional problems).
6) Given polynomials 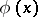 and
and  ,
, 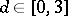 ,
, 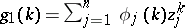 and
and 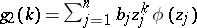 , determine
, determine
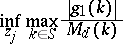 |
and
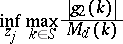 |
(two-sided direct operator problems).
7) Given a domain 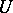 and
and 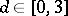 , find
, find
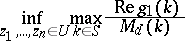 |
and
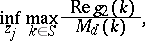 |
where 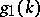 and
and 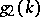 are as above (one-sided conditional operator problems).
are as above (one-sided conditional operator problems).
8) Given a finite set 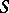 of integers, fixed complex numbers
of integers, fixed complex numbers 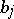 ,
, 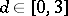 , and two generalized power sums
, and two generalized power sums 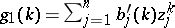 ,
, 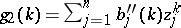 , how large can the quantities
, how large can the quantities
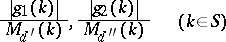 |
be made simultaneously depending only on 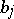 ,
, 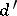 ,
, 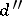 ,
,  , and
, and 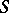 (simultaneous problems)?
(simultaneous problems)?
9) Given two finite sets of integers 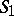 and
and 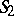 , fixed complex numbers
, fixed complex numbers 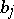 ,
, 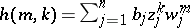 ,
, 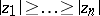 ,
, 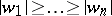 , and
, and 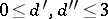 , what is
, what is
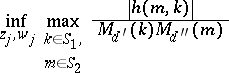 |
and what are the extremal systems (several variables problems)?
Turán and others obtained some lower bounds for some of the above problems.
Let 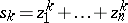 be a pure power sum. Then
be a pure power sum. Then
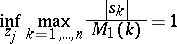 |
and
 |
(see also [a4]). These results were obtained in the equivalent form with 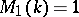 and
and 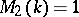 , respectively.
, respectively.
Also, let 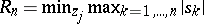 , where
, where 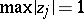 . Then
. Then
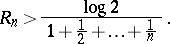 | (a2) |
F.V. Atkinson [a2] improved this by showing that 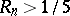 . A. Biro [a3] proved that
. A. Biro [a3] proved that 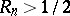 and that if
and that if 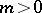 is such that
is such that 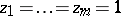 ,
, 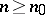 , then
, then
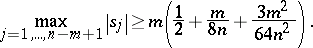 |
J. Anderson [a1] showed that if  , then
, then 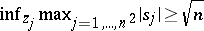 , and that if
, and that if 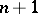 is a prime number, then this
is a prime number, then this  lies in
lies in 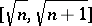 ; he also proved that if
; he also proved that if 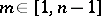 , then there exists a
, then there exists a 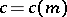 such that
such that
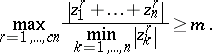 |
It is also known [a43] that, on the other hand, 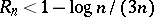 for infinitely many
for infinitely many  and that
and that 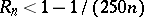 for large enough
for large enough  .
.
P. Erdös proved that
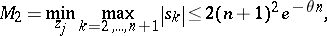 |
where 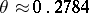 is the solution of the equation
is the solution of the equation 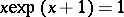 , and L. Erdös [a15] proved that if
, and L. Erdös [a15] proved that if  is large enough, then
is large enough, then 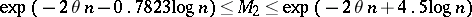 , where
, where 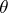 is the solution of the equation
is the solution of the equation 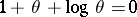 .
.
E. Makai [a44] showed that
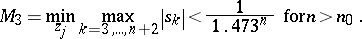 |
For generalized power sums 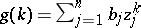 , Turán proved that if
, Turán proved that if 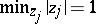 , then
, then
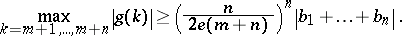 |
Makai [a45] and N.G. de Bruijn [a4] proved, independently, that 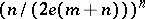 can be replaced with
can be replaced with  , where
, where 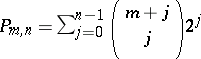 . If, however, one replaces it with
. If, however, one replaces it with 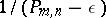 for any
for any  , then the above inequality fails. Turán also proved that if
, then the above inequality fails. Turán also proved that if 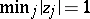 , then
, then
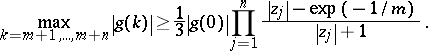 |
G. Halasz showed that for any 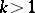 ,
,
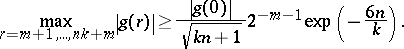 |
S. Gonek [a18] proved that for all 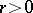 ,
,
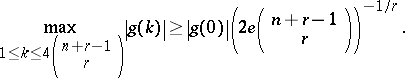 |
In the case of the maximum norm, V. Sos and Turán [a46] obtained the following result. Let  . Then for any integer
. Then for any integer 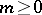 ,
,
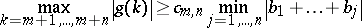 |
with 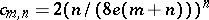 . G. Kolesnik and E.G. Straus [a42] improved this by showing that one can take
. G. Kolesnik and E.G. Straus [a42] improved this by showing that one can take 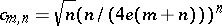 . On the other hand, Makai [a45] showed that for
. On the other hand, Makai [a45] showed that for
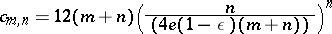 |
the inequality fails for some 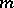 and
and 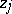 .
.
Considering different ranges for 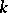 , Halasz [a19] proved that if
, Halasz [a19] proved that if 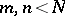 , then
, then
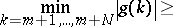 |
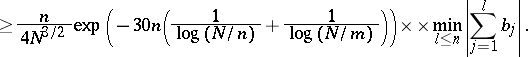 |
Other norms and conditions.
The following results are obtained for two-sided problems with other norms and conditions.
A) ([a17], [a47], [a8], [a45]). Let 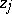 be ordered so that
be ordered so that 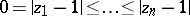 . Assume that
. Assume that 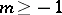 and
and 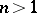 . Then
. Then
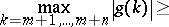 |
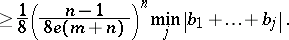 |
B) ([a91]). Let 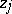 be ordered as in A). Assume that
be ordered as in A). Assume that 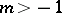 and
and 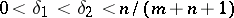 , let
, let  be the largest integer satisfying
be the largest integer satisfying 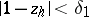 and let
and let 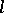 be the smallest integer satisfying
be the smallest integer satisfying  (if such an integer does not exist, take
(if such an integer does not exist, take 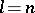 ). Then
). Then
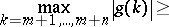 |
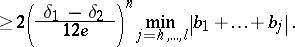 |
C) ([a12]). Let 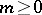 and let
and let 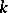 ,
, 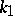 ,
,  be such that
be such that
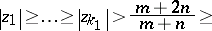 |
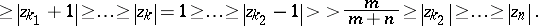 |
Then
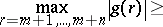 |
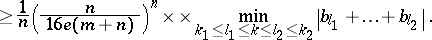 |
D) ([a59]). If 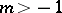 and
and 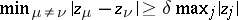 , then
, then
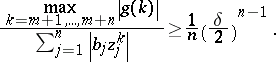 |
E) ([a8]). If 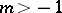 and
and  is such that
is such that 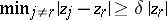 , then there exists a
, then there exists a  such that
such that
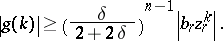 |
F) ((Halasz). Let  and
and  be non-negative integers,
be non-negative integers, 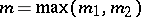 , and
, and 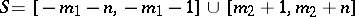 . Assume that
. Assume that 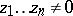 . Then there exists an integer
. Then there exists an integer 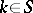 such that
such that
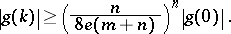 |
G) (Turán). If 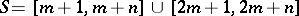 , then the above inequality holds with
, then the above inequality holds with 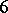 instead of
instead of 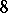 .
.
Problems of type 3) and 7).
Assume that 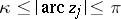 ,
, 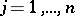 , with
, with 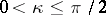 , let
, let 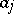 be real numbers, and let
be real numbers, and let 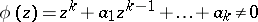 for
for 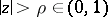 . Define
. Define 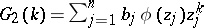 for some fixed complex numbers
for some fixed complex numbers 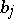 . Assuming that
. Assuming that 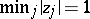 , Turán proved that
, Turán proved that 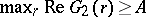 and
and 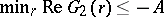 , where
, where
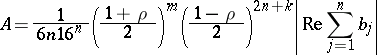 |
and the minimum is taken over all integers 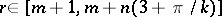 .
.
If 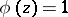 , then the above inequalities hold with
, then the above inequalities hold with
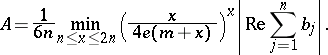 |
Also, if 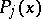 are polynomials of degree
are polynomials of degree 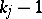 ,
, 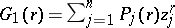 and
and 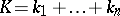 , then
, then 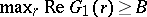 and
and  , where
, where
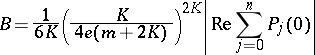 |
and the range of  is
is 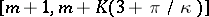 .
.
Assume now that 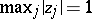 . Let
. Let 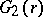 be as defined above, and assume
be as defined above, and assume 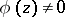 for
for 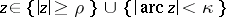 , where
, where 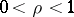 and
and 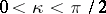 . Assume also that
. Assume also that 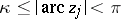 ,
, 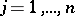 . Take any
. Take any 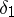 ,
, 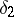 satisfying
satisfying  and define
and define 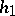 ,
, 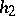 by
by
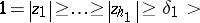 |
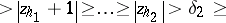 |
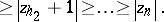 |
(If 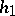 or
or 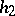 do not exist, replace them with
do not exist, replace them with  .) Put
.) Put 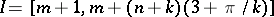 and
and
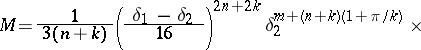 |
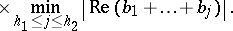 |
Then 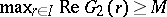 and
and 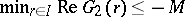 . If
. If 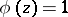 , then the above result holds with
, then the above result holds with 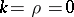 .
.
J.D. Buchholtz [a5], [a6] proved that if 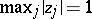 , then
, then
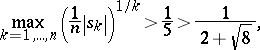 |
respectively, where the last result is the best possible.
R. Tijdeman [a47] proved the following result for "operator-type problems" .
Let 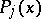 be fixed complex polynomials of degree
be fixed complex polynomials of degree 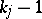 and let
and let 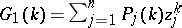 . Then for every integer
. Then for every integer 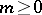 ,
, 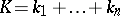 , and
, and 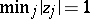 , the inequality
, the inequality
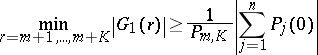 | (a3) |
holds, where 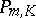 is defined above and the factor
is defined above and the factor 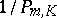 is the best possible; also, if
is the best possible; also, if 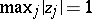 , then (a3) holds with
, then (a3) holds with 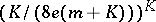 instead of
instead of  .
.
J. Geysel [a17] improved the above constant to
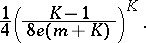 |
Turán studied the other "operator-type problem" for 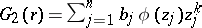 . Let
. Let 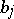 be fixed complex numbers and let
be fixed complex numbers and let 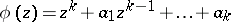 be a polynomial with no zeros outside
be a polynomial with no zeros outside 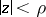 . Assume that
. Assume that 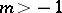 ,
, 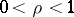 and
and  . Then
. Then
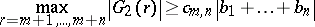 | (a4) |
with
 |
In case of the maximum norm and 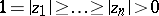 , Turán proved (a4) with
, Turán proved (a4) with
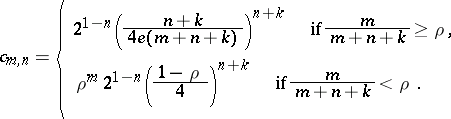 |
He also proved the following "simultaneous problem" . Let 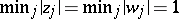 . For any integers
. For any integers 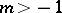 and
and 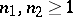 there exist a
there exist a 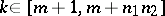 such that the inequalities
such that the inequalities
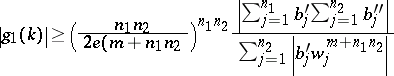 |
and
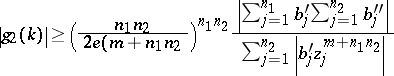 |
hold simultaneously.
References
| [a1] | J. Anderson, "On some power sum problems of Turan and Erdos" Acta Math. Hung. , 70 : 4 (1996) pp. 305–316 |
| [a2] | F.V. Atkinson, "Some further estimates concerning sums of powers of complex numbers" Acta Math. Hung. , XX : 1–2 (1969) pp. 193–210 |
| [a3] | A. Biro, "On a problem of Turan concerning sums of powers of complex numbers" Acta Math. Hung. , 65 : 3 (1994) pp. 209–216 |
| [a4] | N.G. de Bruijn, "On Turan's first main theorem" Acta Math. Hung. , XI : 3–4 (1960) pp. 213–216 |
| [a5] | J.D. Buchholtz, "Extremal problems for sums of powers of complex numbers" Acta Math. Hung. , XVII (1966) pp. 147–153 |
| [a6] | J.D. Buchholtz, "Sums of complex numbers" J. Math. Anal. Appl. , 17 (1967) pp. 269–279 |
| [a7] | J.W.S. Cassels, "On the sums of powers of complex numbers" Acta Math. Hung. , VII : 3–4 (1956) pp. 283–290 |
| [a8] | S. Dancs, "On generalized sums of powers of complex numbers" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , VII (1964) pp. 113–121 |
| [a9] | S. Dancs, P. Turan, "On the distribution of values of a class of entire functions I" Publ. Math. Debrecen , 11 : 1–4 (1964) pp. 257–265 |
| [a10] | S. Dancs, P. Turan, "On the distribution of values of a class of entire functions II" Publ. Math. Debrecen , 11 (1964) pp. 266–272 |
| [a11] | S. Dancs, P. Turan, "Investigations in the power sum theory I" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , XVI (1973) pp. 47–52 |
| [a12] | S. Dancs, P. Turan, "Investigations in the power sum theory II" Acta Arith. , XXV (1973) pp. 105–113 |
| [a13] | S. Dancs, P. Turan, "Investigations in the power sum theory III" Ann. Mat. Pura Appl. , CIII (1975) pp. 199–205 |
| [a14] | S. Dancs, P. Turan, "Investigations in the power sum theory IV" Publ. Math. Debrecen , 22 (1975) pp. 123–131 |
| [a15] | L. Erdös, "On some problems of P. Turan concerning power sums of complex numbers" Acta Math. Hung. , 59 : 1–2 (1992) pp. 11–24 |
| [a16] | P. Erdos, P. Turan, "On a problem in the theory of uniform distribution I and II" Indag. Math. , X : 5 (1948) pp. 3–11; 12–19 |
| [a17] | J.M. Geysel, "On generalized sums of powers of complex numbers" M.C. Report Z.W. (Math. Centre, Amsterdam) , 1968–013 (1968) |
| [a18] | S.M. Gonek, "A note on Turan's method" Michigan Math. J. , 28 : 1 (1981) pp. 83–87 |
| [a19] | G. Halasz, "On the first and second main theorem in Turan's theory of power sums" , Studies Pure Math. , Birkhäuser (1983) pp. 259–269 |
| [a20] | G. Halasz, P. Turan, "On the distribution of roots or Riemann zeta and allied problems I" J. Number Th. , I (1969) pp. 122–137 |
| [a21] | G. Halasz, P. Turan, "On the distribution of roots or Riemann zeta and allied problems II" Acta Math. Hung. , XXI : 3–4 (1970) pp. 403–419 |
| [a22] | S. Knapowski, P. Turan, "The comparative theory of primes I" Acta Math. Hung. , XIII : 3–4 (1962) pp. 299–314 |
| [a23] | S. Knapowski, P. Turan, "The comparative theory of primes II" Acta Math. Hung. , XIII (1962) pp. 315–342 |
| [a24] | S. Knapowski, P. Turan, "The comparative theory of primes III" Acta Math. Hung. , XIII (1962) pp. 343–364 |
| [a25] | S. Knapowski, P. Turan, "The comparative theory of primes IV" Acta Math. Hung. , XIV : 1–2 (1963) pp. 31–42 |
| [a26] | S. Knapowski, P. Turan, "The comparative theory of primes V" Acta Math. Hung. , XIV (1963) pp. 43–64 |
| [a27] | S. Knapowski, P. Turan, "The comparative theory of primes VI" Acta Math. Hung. , XIV (1963) pp. 65–78 |
| [a28] | S. Knapowski, P. Turan, "The comparative theory of primes VII" Acta Math. Hung. , XIV : 3–4 (1963) pp. 241–250 |
| [a29] | S. Knapowski, P. Turan, "The comparative theory of primes VIII" Acta Math. Hung. , XIV (1963) pp. 251–268 |
| [a30] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory I" Acta Arith. , IX : 1 (1964) pp. 23–40 |
| [a31] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory II" Acta Arith. , IX : 3 (1964) pp. 293–314 |
| [a32] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory III" Acta Arith. , XI : 1 (1965) pp. 115–127 |
| [a33] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory IV" Acta Arith. , XI : 2 (1965) pp. 147–162 |
| [a34] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory V" Acta Arith. , XI (1965) pp. 193–202 |
| [a35] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory VI" Acta Arith. , XII : 1 (1966) pp. 85–96 |
| [a36] | S. Knapowski, P. Turan, "Further developments in the comparative prime number theory VII" Acta Arith. , XXI (1972) pp. 193–201 |
| [a37] | S. Knapowski, P. Turan, "On the sign changes of  " Topics in Number Theory (Colloq. Math. Soc. J. Bolyai) , 13 (1976) pp. 153–170 " Topics in Number Theory (Colloq. Math. Soc. J. Bolyai) , 13 (1976) pp. 153–170 |
| [a38] | S. Knapowski, P. Turan, "On the sign changes of 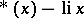 II" Monatsh. Math. , 82 (1976) pp. 163–175 II" Monatsh. Math. , 82 (1976) pp. 163–175 |
| [a39] | S. Knapowski, P. Turan, "On an assertion of Cebysev" J. d'Anal. Math. , XIV (1965) pp. 267–274 |
| [a40] | S. Knapowski, P. Turan, "Uber einige Fragen der vergleichenden Primzahltheorie" , Abhandl. aus der Zahlentheorie und Analysis , VEB Deutsch. Verlag Wiss. (1968) pp. 159–171 |
| [a41] | S. Knapowski, P. Turan, "On prime numbers 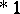 resp. resp. 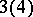 " H. Zassenhaus (ed.) , Number Theory and Algebra , Acad. Press (1977) pp. 157–166 " H. Zassenhaus (ed.) , Number Theory and Algebra , Acad. Press (1977) pp. 157–166 |
| [a42] | G. Kolesnik, E.G. Straus, "On the sum of powers of complex numbers" , Studies Pure Math. , Birkhäuser (1983) pp. 427–442 |
| [a43] | J. Komlos, A. Sarcozy, E. Szemeredi, "On sums of powers of complex numbers" Mat. Lapok , XV : 4 (1964) pp. 337–347 (In Hungarian) |
| [a44] | E. Makai, "An estimation in the theory of diophantine approximations" Acta Math. Hung. , IX : 3–4 (1958) pp. 299–307 |
| [a45] | E. Makai, "On a minimum problem" Acta Math. Hung. , XV : 1–2 (1964) pp. 63–66 |
| [a46] | V.T. Sos, P. Turan, "On some new theorems in the theory of diophantine approximations" Acta Math. Hung. , VI : 3–4 (1955) pp. 241–257 |
| [a47] | R. Tijdeman, "On the distribution of the values of certain functions" PhD Thesis Univ. Amsterdam (1969) |
| [a48] | P. Turan, "Ueber die Verteilung der Primzahlen I" Acta Sci. Math. (Szeged) , X (1941) pp. 81–104 |
| [a49] | P. Turan, "On a theorem of Littlewood" J. London Math. Soc. , 21 (1946) pp. 268–275 |
| [a50] | P. Turan, "Sur la theorie des fonctions quasianalytiques" C.R. Acad. Sci. Paris (1947) pp. 1750–1752 |
| [a51] | P. Turan, "On the gap theorem of Fabry" Acta Math. Hung. , I (1947) pp. 21–29 |
| [a52] | P. Turan, "On Riemann's hypotesis" Acad. Sci. URSS Bull. Ser. Math. , 11 (1947) pp. 197–262 |
| [a53] | P. Turan, "On a new method in the analysis with applications" Casopis Pro Pest. Mat. A Fys. Rc. , 74 (1949) pp. 123–131 |
| [a54] | P. Turan, "On the remainder term of the prime-number formula I" Acta Math. Hung. , I : 1 (1950) pp. 48–63 |
| [a55] | P. Turan, "On the remainder term of the prime-number formula II" Acta Math. Hung. , I : 3–4 (1950) pp. 155–166 |
| [a56] | P. Turan, "On approximate solution of algebraic equations" Publ. Math. Debrecen. , II : 1 (1951) pp. 28–42 |
| [a57] | P. Turan, "On Carlson's theorem in the theory of zetafunction of Riemann" Acta Math. Hung. , II : 1–2 (1951) pp. 39–73 |
| [a58] | P. Turan, "On a property of lacunary power-series" Acta Sci. Math. (Szeged) , XIV : 4 (1952) pp. 209–218 |
| [a59] | P. Turan, "Uber eine neue Methode der Analysis und ihre Anwendungen" , Akad. Kiado (1953) |
| [a60] | P. Turan, "On Lindelof's conjecture" Acta Math. Hung. , V : 3–4 (1954) pp. 145–153 |
| [a61] | P. Turan, "Uber eine neue Methode der Analysis und ihre Anwendungen" , Akad. Kiado (1956) (Rev. Chinese ed.) |
| [a62] | P. Turan, "On the instability of systems of differential equations" Acta Math. Hung. , VI : 3–4 (1955) pp. 257–271 |
| [a63] | P. Turan, "On the zeros of the zetafunction of Riemann" J. Indian Math. Soc. , XX (1956) pp. 17–36 |
| [a64] | P. Turan, "Uber eine neue Methode der Analysis" Wissenschaftl. Z. Humboldt Univ. Berlin (1955/56) pp. 275–279 |
| [a65] | P. Turan, "Uber eine Anwendung einer neuen Methode auf die Theorie der Riemannschen Zetafunktion" Wissenschaftl. Z. Humboldt Univ. Berlin (1955/56) pp. 281–285 |
| [a66] | P. Turan, "Remark on the preceding paper of J.W.S. Cassels" Acta Math. Hung. , VII : 3–4 (1957) pp. 291–294 |
| [a67] | P. Turan, "Remark on the theory of quasianalytic function classes" Publ. Math. Inst. Hung. Acad. Sci. , I : 4 (1956) pp. 481–487 |
| [a68] | P. Turan, "Uber lakunaren Potenzreihen" Rev. Math. Pures Appl. , I (1956) pp. 27–32 |
| [a69] | P. Turan, "On the so-called density hypothesis of zeta-function of Riemann" Acta Arith. , IV : 1 (1958) pp. 31–56 |
| [a70] | P. Turan, "Zur Theorie der Dirichletschen Reihen" Euler Festschr. (1959) pp. 322–336 |
| [a71] | P. Turan, "On a property of the stable or conditionally stable solutions of systems of nonlinear differential equations" Ann. of Math. , XLVIII (1959) pp. 333–340 |
| [a72] | P. Turan, "A note on the real zeros of Dirichlet L-functions" Acta Arith. , V (1959) pp. 309–314 |
| [a73] | P. Turan, "On the distribution of zeros of general exponential polynomials" Publ. Math. Debrecen. , VII (1960) pp. 130–136 |
| [a74] | P. Turan, "On an improvement of some new one-sided theorems of the theory of diophantine approximations" Acta Math. Hung. , XI : 3–4 (1960) pp. 299–316 |
| [a75] | P. Turan, "On a density theorem of Ju.V. Linnik" Publ. Math. Inst. Hung. Acad. Sci. Ser.A , VI : 1–2 (1961) pp. 165–179 |
| [a76] | P. Turan, "On the eigenvalues of matrices" Ann. Mat. Pura Appl. , IV (LIV) (1961) pp. 397–401 |
| [a77] | P. Turan, "On some further one-sided theorems of new type" Acta Math. Hung. , XII : 3–4 (1961) pp. 455–468 |
| [a78] | P. Turan, "A remark on the heat equation" J. d'Anal. Math. , XIV (1965) pp. 443–448 |
| [a79] | P. Turan, "On a certain limitation of eigenvalues of matrices" Aequat. Math. , 2 : 2–3 (1969) pp. 184–189 |
| [a80] | P. Turan, "On the approximate solutions of algebraic equations" Commun. Math. Phys. Class Hung. Acad. , XVIII (1968) pp. 223–236 (In Hungarian) |
| [a81] | P. Turan, "A remark on linear differential equations" Acta Math. Hung. , XX : 3–4 (1969) pp. 357–360 |
| [a82] | P. Turan, "Zeta roots and prime numbers" Colloq. Math. Soc. Janos Bolyai (Number Theory) , 2 (1969) pp. 205–216 |
| [a83] | P. Turan, "Exponential sums and the Riemann conjecture" , Analytic Number Theory , Proc. Symp. Pure Math. , XXIV , Amer. Math. Soc. (1973) pp. 305–314 |
| [a84] | P. Turan, "On an inequality of Cebysev" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , XI (1968) pp. 15–16 |
| [a85] | P. Turan, "On an inequality" Ann. Univ. Sci. Budapest. Eotvos Sect. Math. , I (1958) pp. 3–6 |
| [a86] | P. Turan, "On a certain problem in the theory of power series with gaps" , Studies Math. Anal. Rel. Topics , Stanford Univ. Press (1962) pp. 404–409 |
| [a87] | P. Turan, "On a trigonometric inequality" , Proc. Constructive Theory of Functions , Akad. Kiado (1969) pp. 503–512 |
| [a88] | P. Turan, "Investigations in the power sum theory II (with S. Dancs)" Acta Arith. , XXV (1973) pp. 105–113 |
| [a89] | P. Turan, "On the latent roots of  -matrices" Comput. Math. Appl. (1975) pp. 307–313 -matrices" Comput. Math. Appl. (1975) pp. 307–313 |
| [a90] | P. Turan, "On some recent results in the analytical theory of numbers" , Proc. Symp. Pure Math. , XX , Inst. Number Theory (1969) pp. 359–374 |
| [a91] | P. Turan, "On a new method of analysis and its applications" , Wiley (1984) |
Turán theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tur%C3%A1n_theory&oldid=15479