Tube domain
From Encyclopedia of Mathematics
tube
A domain 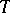 in the complex space
in the complex space 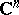 of the form
of the form
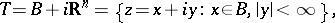 |
where 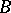 is a domain in the real subspace
is a domain in the real subspace 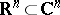 , called the base of the tube domain
, called the base of the tube domain 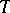 . A domain of the form
. A domain of the form 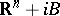 is also called a tube domain. The holomorphic envelope of an arbitrary tube domain is the same as its convex hull; in particular, every function that is holomorphic in a tube domain
is also called a tube domain. The holomorphic envelope of an arbitrary tube domain is the same as its convex hull; in particular, every function that is holomorphic in a tube domain 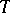 can be extended to a function that is holomorphic in the convex hull of
can be extended to a function that is holomorphic in the convex hull of 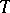 . A tube domain is said to be radial if its base is a connected cone in
. A tube domain is said to be radial if its base is a connected cone in 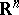 .
.
References
| [1] | V.S. Vladimirov, "Methods of the theory of functions of many complex variables" , M.I.T. (1966) (Translated from Russian) |
Comments
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4 |
How to Cite This Entry:
Tube domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tube_domain&oldid=15666
Tube domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tube_domain&oldid=15666
This article was adapted from an original article by E.M. Chirka (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article