Trigonometric series
A series in cosines and sines of multiple angles, that is, a series of the form
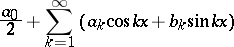 | (1) |
or, in complex form,
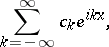 |
where 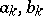 or, respectively,
or, respectively, 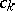 are called the coefficients of the trigonometric series.
are called the coefficients of the trigonometric series.
Trigonometric series are first encountered in the work of L. Euler (1744). He obtained the expansions
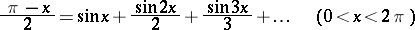 |
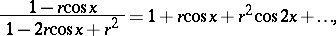 |
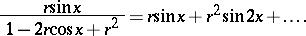 |
In the middle of the 18th century, in connection with the study of problems on the free oscillations of strings, there arose the question of the possibility of "representing" functions characterizing the initial position of a string in the form of a sum of a trigonometric series. This question raised fierce debates, continuing over several decades, among the best analysts of that time, such as D. Bernoulli, J. d'Alembert, J.L. Lagrange, and Euler. These arguments related to the essence of the notion of a function. At that time, functions were usually related to their analytic specifications, which led to the consideration of analytic or piecewise-analytic functions only. But here the need arose to construct a trigonometric series "representing" a function whose graph could be a rather arbitrary curve.
However, the significance of the arguments was even greater. In fact, out of these discussions various questions arose connected with many fundamentally important concepts and ideas of mathematical analysis in general, such as the "representation" of functions by Taylor series and the analytic continuation of functions, the use of divergent series, interchange of limits, infinite systems of equations, interpolation of functions by polynomials, etc.
Subsequently, as well as in this initial period, the theory of trigonometric series served as a source of new ideas of mathematical analysis and influenced the development of other branches of it. Investigations in trigonometric series played an important role in the construction of the Riemann and Lebesgue integrals. The theory of functions of a real variable originated and was then developed in close connection with the theory of trigonometric series. As generalizations of the theory of trigonometric series there emerged the Fourier integral, almost-periodic functions, general orthogonal series, and abstract harmonic analysis. Research into trigonometric series served as a starting point in the creation of set theory. Trigonometric series are a powerful means for representing and studying functions.
The question introduced into the debates of the mathematicians in the 18th century was solved in 1807 by J. Fourier, who gave formulas for calculating the coefficients of the trigonometric series (1) that had to "represent" a function 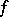 on
on 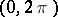 :
:
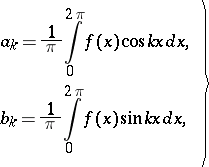 | (2) |
and who applied them in the solution of problems of heat conduction. Formulas (2) have acquired the name Fourier formulas, although they were encountered earlier by A. Clairaut (1754) and Euler (1777) via term-by-term integration. The trigonometric series (1) whose coefficients are defined by (2) is called the Fourier series of 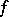 , and the numbers
, and the numbers 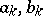 the Fourier coefficients of
the Fourier coefficients of 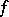 .
.
The character of the results obtained depends on how the "representation" of the function by a series is to be understood, and how the integral in (2) is to be understood. The modern form of the theory of trigonometric series was obtained after the appearance of the Lebesgue integral.
The theory of trigonometric series can conditionally be divided into two main branches: the theory of Fourier series, in which it is supposed that the series (1) is the Fourier series of some function, and the theory of general trigonometric series, where this hypothesis is not made. The main results in the theory of general trigonometric series are given below (here the measure of sets and measurability of functions are to be understood in the sense of Lebesgue).
The first systematic study of trigonometric series in which it was not supposed that these series are Fourier series, was the dissertation of B. Riemann (1853). For this reason, the theory of general trigonometric series is sometimes called the Riemann theory of trigonometric series.
For the study of the properties of an arbitrary series (1) with coefficients converging to zero, Riemann considered the continuous function 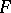 that is the sum of the uniformly-convergent series
that is the sum of the uniformly-convergent series
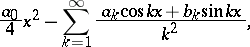 |
obtained after twice term-by-term integration of the series (1). If the series (1) converges at some point  to the number
to the number  , then the second symmetric derivative of
, then the second symmetric derivative of 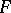 exists at this point and is equal to
exists at this point and is equal to  :
:
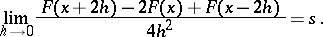 |
Since
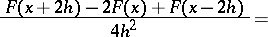 |
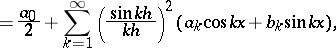 |
this leads to the summation of (1) produced by the factors 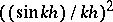 , called the Riemann summation method. By means of the function
, called the Riemann summation method. By means of the function 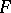 , Riemann formulated the localization principle, according to which the behaviour of the series (1) at a point
, Riemann formulated the localization principle, according to which the behaviour of the series (1) at a point  depends only on the behaviour of
depends only on the behaviour of 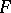 in an arbitrarily small neighbourhood of this point.
in an arbitrarily small neighbourhood of this point.
If a trigonometric series converges on a set of positive measure, then its coefficients converge to zero (the Cantor–Lebesgue theorem). Convergence to zero of the coefficients of a trigonometric series also follows from convergence of the series on a set of the second category (W. Young, 1909).
One of the central problems in the theory of general trigonometric series is that of "representing" an arbitrary function by a trigonometric series. By strengthening results of N.N. Luzin (1915) on the representation of functions by trigonometric series that are summable almost-everywhere by the methods of Abel–Poisson and Riemann, D.E. Men'shov proved (1940) the following theorem, relating to the most important case when the representation of 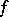 is understood as convergence of the trigonometric series to
is understood as convergence of the trigonometric series to 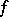 almost everywhere. There exists for any measurable, almost-everywhere finite
almost everywhere. There exists for any measurable, almost-everywhere finite 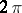 -periodic function
-periodic function 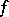 a trigonometric series converging to it almost-everywhere (Men'shov's theorem). It should be noted that even if the function
a trigonometric series converging to it almost-everywhere (Men'shov's theorem). It should be noted that even if the function 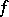 is integrable, one cannot in general choose the Fourier series of
is integrable, one cannot in general choose the Fourier series of 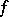 for this series, since there exist Fourier series that are everywhere divergent.
for this series, since there exist Fourier series that are everywhere divergent.
Men'shov's theorem can be strengthened as follows: If a 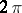 -periodic function
-periodic function 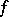 is measurable and finite almost everywhere, then there exists a continuous function
is measurable and finite almost everywhere, then there exists a continuous function 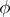 such that
such that 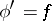 almost everywhere and the differentiated Fourier series of
almost everywhere and the differentiated Fourier series of 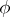 converges to
converges to 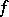 almost everywhere (N.K. Bari, 1952).
almost everywhere (N.K. Bari, 1952).
It is not known (1984) whether the condition that 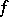 be finite almost-everywhere can be dropped in Men'shov's theorem. In particular, it is not known (1984) whether there is a trigonometric series converging almost-everywhere to
be finite almost-everywhere can be dropped in Men'shov's theorem. In particular, it is not known (1984) whether there is a trigonometric series converging almost-everywhere to 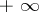 .
.
Therefore the problem on the representation of functions that can take infinite values on a set of positive measure has been considered for the case when convergence almost-everywhere is replaced by a weaker condition, namely, convergence in measure. Convergence in measure to functions that can take infinite values is defined as follows: The sequence 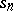 of partial sums of a trigonometric series converges in measure to a function
of partial sums of a trigonometric series converges in measure to a function 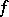 if
if
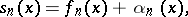 |
where 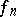 converges to
converges to 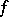 almost everywhere, while the sequence
almost everywhere, while the sequence 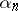 converges in measure to zero. In this formulation, the question of the representation of functions has been completely solved: there exists for any measurable
converges in measure to zero. In this formulation, the question of the representation of functions has been completely solved: there exists for any measurable 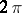 -periodic function a trigonometric series converging to it in measure (Men'shov, 1948).
-periodic function a trigonometric series converging to it in measure (Men'shov, 1948).
Much research has been devoted to the problem of uniqueness of trigonometric series: Can two distinct trigonometric series converge to the same function? In another formulation: If a trigonometric series converges to zero, then does it follow that all coefficients of the series are zero? Here one may have in mind convergence at all points or at all points outside some set. The answers to these questions depend essentially on the properties of the set outside which convergence is presupposed.
The following terminology has been established. A set 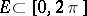 is called a set of uniqueness (cf. Uniqueness set), or a
is called a set of uniqueness (cf. Uniqueness set), or a 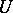 -set, if the convergence everywhere on
-set, if the convergence everywhere on 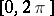 of a trigonometric series to zero except, perhaps, at points of
of a trigonometric series to zero except, perhaps, at points of 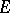 , implies that all coefficients of the series are zero. Otherwise
, implies that all coefficients of the series are zero. Otherwise 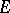 is called a set of multiplicity, or an
is called a set of multiplicity, or an 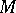 -set. As G. Cantor showed (1872), the empty, as well as any finite, set is a
-set. As G. Cantor showed (1872), the empty, as well as any finite, set is a 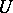 -set. Any countable set is also a
-set. Any countable set is also a 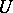 -set (Young, 1909). On the other hand, every set of positive measure is an
-set (Young, 1909). On the other hand, every set of positive measure is an 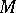 -set.
-set.
The existence of 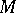 -sets of measure zero was established by Men'shov (1916), who constructed the first example of a perfect set possessing these properties. This result is of prime importance in the uniqueness problem. It follows from the existence of
-sets of measure zero was established by Men'shov (1916), who constructed the first example of a perfect set possessing these properties. This result is of prime importance in the uniqueness problem. It follows from the existence of 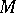 -sets of measure zero that in the representation of functions by trigonometric series converging almost everywhere, these series are automatically non-uniquely determined.
-sets of measure zero that in the representation of functions by trigonometric series converging almost everywhere, these series are automatically non-uniquely determined.
Perfect sets can also be 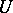 -sets (Bari; A. Rajchman, 1921). In the uniqueness problem, an important role is played by very precise characteristics of sets of measure zero. The general question on the classification of sets of measure zero into
-sets (Bari; A. Rajchman, 1921). In the uniqueness problem, an important role is played by very precise characteristics of sets of measure zero. The general question on the classification of sets of measure zero into 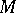 - and
- and 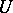 -sets remains open (1984). It has not even been solved for perfect sets.
-sets remains open (1984). It has not even been solved for perfect sets.
The following problem touches on the uniqueness problem. If a trigonometric series converges to a function 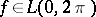 , then does this series have to be the Fourier series of
, then does this series have to be the Fourier series of 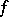 ? P. du Bois-Reymond (1877) gave an affirmative answer to this question when
? P. du Bois-Reymond (1877) gave an affirmative answer to this question when 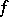 is Riemann integrable and the series converges to
is Riemann integrable and the series converges to 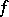 at all points. Results of Ch.J. de la Vallée-Poussin (1912) imply that the answer is also affirmative in case the series is convergent to a finite sum everywhere except on a countable set of points.
at all points. Results of Ch.J. de la Vallée-Poussin (1912) imply that the answer is also affirmative in case the series is convergent to a finite sum everywhere except on a countable set of points.
If a trigonometric series converges absolutely at some point 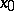 , then the points of convergence of the series, as well as the points of its absolute convergence, are distributed symmetrically about
, then the points of convergence of the series, as well as the points of its absolute convergence, are distributed symmetrically about 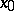 (P. Fatou, 1906).
(P. Fatou, 1906).
According to the Denjoy–Luzin theorem, absolute convergence on a set of positive measure of a trigonometric series (1) implies that the series 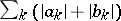 is convergent, and hence that (1) is absolutely convergent for all
is convergent, and hence that (1) is absolutely convergent for all  . This property is also possessed by sets of the second category and certain sets of measure zero.
. This property is also possessed by sets of the second category and certain sets of measure zero.
This survey only covers one-dimensional trigonometric series (1). There are separate results relating to general trigonometric series of several variables. Here in many cases it is also necessary to find natural formulations of the problems.
References
| [1] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [3] | N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1951) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212) |
| [4] | B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" H. Weber (ed.) , B. Riemann's Gesammelte Mathematische Werke , Dover, reprint (1953) pp. 227–265 ((Original: Göttinger Akad. Abh.  (1868))) (1868))) |
Comments
For the convergence of Fourier series see also Carleson theorem.
The problems related to Men'shov's theorem cited above that were unsolved in 1984 have now been solved. In [a1], S.V. Konyagin proved the necessity part of the following brilliant theorem. (The sufficiency part had already been proved by D.E. Men'shov (see [a2] or [1], vol. II, p. 437).)
Men'shov–Konyagin theorem. Let 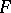 and
and 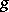 be measurable functions from
be measurable functions from 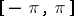 into
into 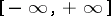 . In order that a trigonometric series (1) having partial sums
. In order that a trigonometric series (1) having partial sums 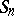 exists for which
exists for which
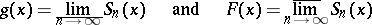 |
for almost-all 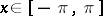 , it is necessary and sufficient that a measurable set
, it is necessary and sufficient that a measurable set 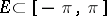 exists such that
exists such that 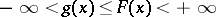 for almost-all
for almost-all 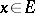 , while
, while 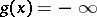 and
and 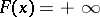 for almost-all
for almost-all 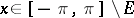 .
.
In particular, no trigonometric series has sum 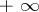 at every point of a set of positive measure.
at every point of a set of positive measure.
References
| [a1] | S.V. Konyagin, "Limits of indeterminacy of trigonometric series" Math. Notes , 44 (1988) pp. 910–920 Mat. Zametki , 44 : 6 (1988) pp. 770–784 |
| [a2] | D.E. Men'shov, "On limits of indeterminacy of Fourier series" Mat. Sb. , 30 : 3 (1952) pp. 601–650 (In Russian) |
Trigonometric series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trigonometric_series&oldid=15507