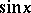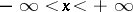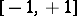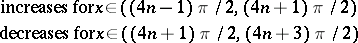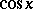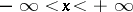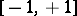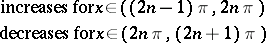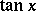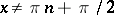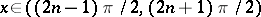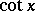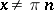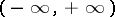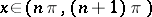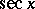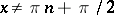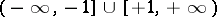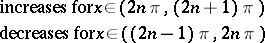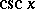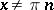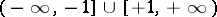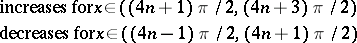Trigonometric functions
The class of elementary functions sine, cosine, tangent, cotangent, secant, cosecant. These are denoted, respectively, by: 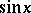 ,
, 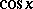 ,
, 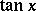 (or
(or 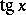 ),
), 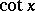 (or
(or 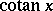 ),
), 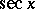 ,
, 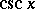 (or
(or 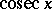 ).
).
Trigonometric functions of a real argument.
Let 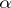 be a real number. Let
be a real number. Let 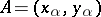 be the end point of the arc on the unit circle
be the end point of the arc on the unit circle 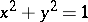 (see Fig. a) having initial point
(see Fig. a) having initial point 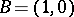 and length
and length 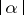 . The arc from
. The arc from 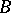 to
to 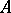 is taken in the counter-clockwise direction if
is taken in the counter-clockwise direction if 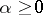 , and in the clockwise direction if
, and in the clockwise direction if 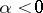 . If
. If 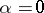 , then
, then 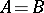 ; if, e.g.,
; if, e.g., 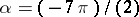 , then
, then 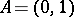 .
. 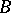 ,
, 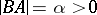

Figure: t094210a
The basic trigonometric functions sine and cosine are defined at  by the formulas
by the formulas
 |
The remaining trigonometric functions can be defined by the formulas
 |
 |
All trigonometric functions are periodic. The graphs of the trigonometric functions are given in Fig. b.
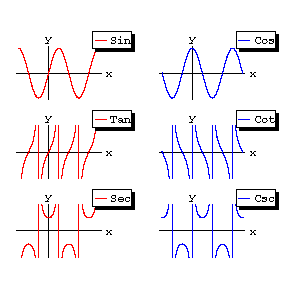
Figure: t094210b
The main properties of the trigonometric functions — the domain of definition, the range, the parity, and sections of monotonicity — are given in the table below.'
<tbody> </tbody>
|
Each trigonometric function is continuous and infinitely differentiable at each point of its domain of definition; the derivatives of the trigonometric functions are:
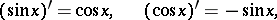 |
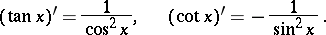 |
The integrals of the trigonometric functions are:
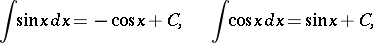 |
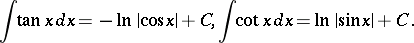 |
All trigonometric functions have a power series expansion:
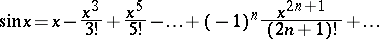 |
for 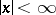 ;
;
 |
for  ;
;
 |
 |
for 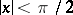 ;
;
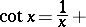 |
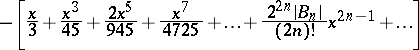 |
for 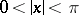 (the
(the 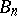 are the Bernoulli numbers).
are the Bernoulli numbers).
The function inverse to the function 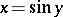 defines
defines 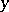 as a many-valued function of
as a many-valued function of  , it is denoted by
, it is denoted by 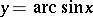 . The inverse functions of the other trigonometric functions are defined similarly; they are all called inverse trigonometric functions.
. The inverse functions of the other trigonometric functions are defined similarly; they are all called inverse trigonometric functions.
Trigonometric functions of a complex variable.
The trigonometric functions for complex values of the variable 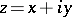 are defined as analytic continuations (cf. Analytic continuation) of the corresponding trigonometric functions of the real variable in the complex plane.
are defined as analytic continuations (cf. Analytic continuation) of the corresponding trigonometric functions of the real variable in the complex plane.
Thus, 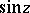 and
and 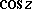 can be defined by means of the power series for
can be defined by means of the power series for 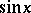 and
and 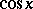 given above. These series converge in the entire complex plane, therefore
given above. These series converge in the entire complex plane, therefore 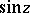 and
and 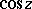 are entire functions (cf. Entire function).
are entire functions (cf. Entire function).
The trigonometric functions tangent and cotangent are defined by the formulas
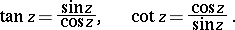 |
The trigonometric functions 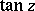 and
and 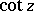 are meromorphic functions (cf. Meromorphic function). The poles of
are meromorphic functions (cf. Meromorphic function). The poles of 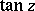 are simple (of order one) and are situated at the points
are simple (of order one) and are situated at the points 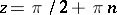 ,
, 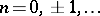 .
.
All formulas for the trigonometric functions of a real argument remain true for a complex argument as well.
In contrast to the trigonometric functions of a real variable, the functions 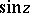 and
and 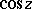 take all complex values: The equations
take all complex values: The equations 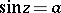 and
and 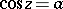 each have infinitely many solutions for any complex
each have infinitely many solutions for any complex  :
:
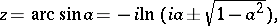 |
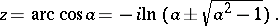 |
The trigonometric functions 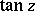 and
and 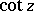 take all complex values except
take all complex values except 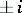 : The equations
: The equations 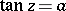 ,
, 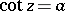 each have infinitely many solutions for any complex number
each have infinitely many solutions for any complex number 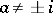 :
:
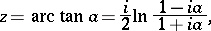 |
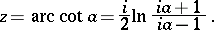 |
The trigonometric functions can be expressed in terms of the exponential function:
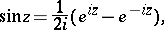 |
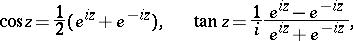 |
and the hyperbolic functions:
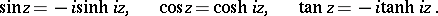 |
Comments
The trigonometric functions are also called circular functions.
A formal definition of 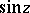 and
and 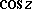 (independent of a picture) can be given by power series and as follows. First of all it can easily be proved that from the previous, visual definition of
(independent of a picture) can be given by power series and as follows. First of all it can easily be proved that from the previous, visual definition of 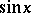 and
and 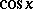 follows:
follows:
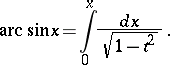 |
This can be taken as a formal definition of 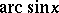 and the inverse function of
and the inverse function of 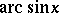 can be taken as a formal definition of
can be taken as a formal definition of  .
.
If  is a complex number
is a complex number 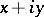 , with real
, with real  and
and 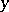 , one can define
, one can define 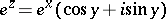 , and then for complex
, and then for complex  define:
define:
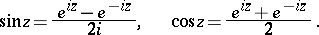 |
References
| [a1] | T.M. Apostol, "Calculus" , I , Blaisdell (1967) |
| [a2] | A.R.F. Verhey, "Complex variables and applications" , McGraw-Hill (1974) |
| [a3] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) |
Trigonometric functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trigonometric_functions&oldid=14919