Trigonalizable element
triangular element
A trigonalizable element of the algebra 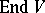 of endomorphisms of a finite-dimensional vector space
of endomorphisms of a finite-dimensional vector space 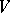 over a field
over a field 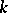 is an element
is an element 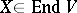 all eigenvalues of which belong to
all eigenvalues of which belong to  . If
. If 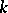 is algebraically closed, then every element of
is algebraically closed, then every element of 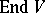 is trigonalizable. For a trigonalizable element
is trigonalizable. For a trigonalizable element 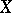 (and only for such an element) there exists a basis in
(and only for such an element) there exists a basis in 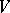 with respect to which the matrix of the endomorphism
with respect to which the matrix of the endomorphism 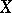 is triangular (or, what is the same, there exists a complete flag in
is triangular (or, what is the same, there exists a complete flag in 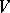 that is invariant with respect to
that is invariant with respect to 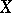 ). A trigonalizable element has a Jordan decomposition over
). A trigonalizable element has a Jordan decomposition over  . There exist a number of generalizations of the notion of a trigonalizable element in
. There exist a number of generalizations of the notion of a trigonalizable element in 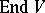 for the case that
for the case that 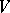 is infinite-dimensional (see ).
is infinite-dimensional (see ).
A trigonalizable element of a finite-dimensional algebra 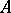 over a field
over a field 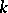 is an element
is an element 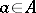 such that the operator of right (or left, depending on the case under consideration) multiplication by
such that the operator of right (or left, depending on the case under consideration) multiplication by  is a trigonalizable element in the algebra
is a trigonalizable element in the algebra 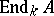 . If
. If 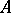 is isomorphic to the algebra
is isomorphic to the algebra  for some finite-dimensional vector space
for some finite-dimensional vector space  over
over 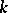 , then these two (formally distinct) definitions reduce to the same concept.
, then these two (formally distinct) definitions reduce to the same concept.
In Lie algebras, trigonalizability of an element 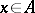 means trigonalizability of the endomorphism
means trigonalizability of the endomorphism 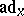 (where
(where 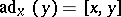 ). The set of all trigonalizable elements in a Lie algebra is, in general, not closed with respect to the operations of addition and commutation (for example, for
). The set of all trigonalizable elements in a Lie algebra is, in general, not closed with respect to the operations of addition and commutation (for example, for 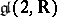 , the simple Lie algebra of real matrices of order 2 with trace 0). However, in the case of a solvable algebra
, the simple Lie algebra of real matrices of order 2 with trace 0). However, in the case of a solvable algebra 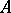 , this set is even a characteristic ideal of
, this set is even a characteristic ideal of 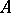 .
.
A trigonalizable element in a connected finite-dimensional Lie group 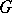 is an element
is an element 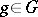 such that
such that 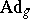 is a trigonalizable element in
is a trigonalizable element in 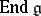 (here
(here 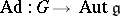 is the adjoint representation of the Lie group
is the adjoint representation of the Lie group 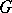 in the group
in the group  of automorphisms of its Lie algebra
of automorphisms of its Lie algebra 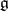 ). If
). If 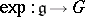 is the exponential mapping and
is the exponential mapping and 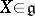 is a trigonalizable element (in the sense of 2)), then
is a trigonalizable element (in the sense of 2)), then 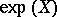 is a trigonalizable element of
is a trigonalizable element of 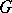 . The converse is, in general, false.
. The converse is, in general, false.
Lie algebras and Lie groups all elements of which are trigonalizable are called trigonalizable algebras or groups, respectively, and also supersolvable Lie algebras, respectively (cf. Lie algebra, supersolvable; Lie group, supersolvable).
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | B.I. Plotkin, "Groups of automorphisms of algebraic systems" , Wolters-Noordhoff (1972) |
| [3] | M.M. Postnikov, "Linear algebra and differential geometry" , Moscow (1979) (In Russian) |
Comments
References
| [a1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
Trigonalizable element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trigonalizable_element&oldid=17777