Trefftz method
One of the variational methods for solving boundary value problems. Suppose one has to solve the boundary value problem
 | (*) |
where 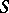 is the boundary of a domain
is the boundary of a domain 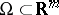 . The solution of the problem (*) minimizes the functional
. The solution of the problem (*) minimizes the functional
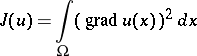 |
over all functions satisfying the boundary condition 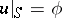 . Trefftz' method consists in the following. Suppose one is given a sequence of harmonic functions
. Trefftz' method consists in the following. Suppose one is given a sequence of harmonic functions 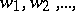 in
in  that are square summable in
that are square summable in  together with their first derivatives. An approximate solution is sought in the form
together with their first derivatives. An approximate solution is sought in the form
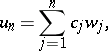 |
the coefficients 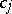 being determined from the condition that
being determined from the condition that 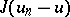 is minimal, where
is minimal, where  is the exact solution of (*). This leads to the following system of equations for
is the exact solution of (*). This leads to the following system of equations for  :
:
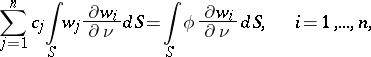 |
where  is the outward normal to
is the outward normal to 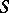 .
.
Trefftz' method can be generalized to various boundary value problems (see [2]–[4]).
The method was proposed by E. Trefftz (see [1]).
References
| [1] | E. Trefftz, "Ein Gegenstück zum Ritzschen Verfahren" , Verhandl. 2er Internat. Kongress. Techn. Mechanik Zürich, 1926, 12–17 Sept. , O. Füssli (1927) pp. 131–137 |
| [2] | S.G. [S.G. Mikhlin] Michlin, "Variationsmethoden der mathematischen Physik" , Akademie Verlag (1962) (Translated from Russian) |
| [3] | V.I. Krylov, V.V. Bobkov, P.I. Monastyrnyi, "Computing methods of higher mathematics" , 2 , Minsk (1975) (In Russian) |
| [4] | M.Sh. Birman, "Variational methods for solving boundary value problems analogous to Trefftz' method" Vestnik Leningrad. Gos. Univ. Ser. mat. Mekh. i Astr. , 11 : 13 (1956) pp. 69–89 (In Russian) |
Comments
References
| [a1] | K. Rektorys (ed.) , Applicable mathematics , Iliffe (1969) pp. 1056–1058 |
Trefftz method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trefftz_method&oldid=12688