Trapezium formula
The special case of the Newton–Cotes quadrature formula in which two nodes are taken:
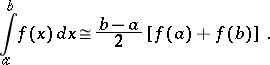 | (1) |
If the integrand 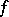 differs strongly from a linear function, then formula (1) is not very exact. In this case the interval
differs strongly from a linear function, then formula (1) is not very exact. In this case the interval 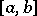 is divided into
is divided into  subintervals
subintervals 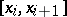 ,
, 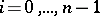 , of length
, of length 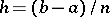 , and for the calculation of the integral over
, and for the calculation of the integral over 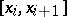 one uses the trapezium formula
one uses the trapezium formula
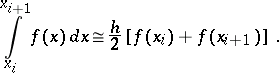 |
Summation of the left- and right-hand sides of this approximate equality with respect to 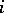 from 0 to
from 0 to 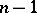 leads to the composite trapezium formula:
leads to the composite trapezium formula:
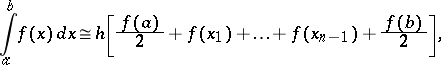 | (2) |
where 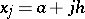 ,
, 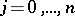 . The quadrature formula (2) is also called the trapezium formula (without adding the word composite). The algebraic degree of accuracy of the quadrature formula (2), as well as of (1), is equal to 1. The quadrature formula (2) is exact for the trigonometric functions
. The quadrature formula (2) is also called the trapezium formula (without adding the word composite). The algebraic degree of accuracy of the quadrature formula (2), as well as of (1), is equal to 1. The quadrature formula (2) is exact for the trigonometric functions
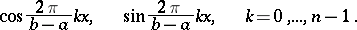 |
In the case when 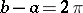 , formula (2) is exact for all trigonometric polynomials of order not exceeding
, formula (2) is exact for all trigonometric polynomials of order not exceeding 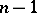 ; furthermore, its trigonometric degree of accuracy is equal to
; furthermore, its trigonometric degree of accuracy is equal to 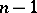 .
.
If the integrand 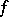 is twice-continuously differentiable on
is twice-continuously differentiable on 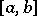 , then the error
, then the error 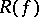 of the quadrature formula (2), that is, the difference between the integral and the quadrature sum, is given by
of the quadrature formula (2), that is, the difference between the integral and the quadrature sum, is given by
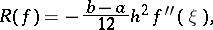 |
where 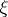 is a point of
is a point of 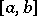 .
.
Comments
The complete formula
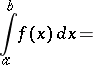 |
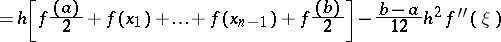 |
is often referred to as the trapezoidal rule.
References
| [a1] | F.B. Hildebrand, "Introduction to numerical analysis" , Dover, reprint (1974) pp. 95ff |
| [a2] | W.H. Press, B.P. Flannery, S.A. Teukolsky, W.T. Vetterling, "Numerical recipes" , Cambridge Univ. Press (1986) pp. 105ff |
Trapezium formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trapezium_formula&oldid=12696